Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 6
Faça um esboço da parábola com equação . Ache (a) o vértice, (b) a equação do eixo, (c) o foco e (d) a equação da diretriz.
Passo 1
Bom, o enunciado nos pede o esboço da parábola com equação que será:
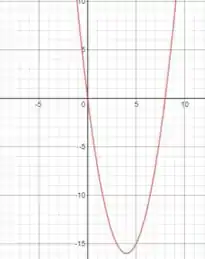
Vamos primeiro reescrever a equação, para que ela fique na forma geral da parábola:
Adicionando 16 nos dois lados:
Completando quadrados:
Passo 2
Como agora sabemos os valores do quanto a parábola foi transladada, podemos encontrar o vértice comparando com a equação geral da parábola:
Assim, o vértice está em , o que responde a letra (a)
Passo 3
Na letra (b), o enunciado pede a equação do eixo, que será paralelo ao eixo y no caso da nossa parábola, logo, ele terá o valor de h, então:
Que descreve uma reta vertical que passa pelo ponto 4.
Passo 4
A letra (c) nos pede o foco que nesse caso pode ser determinado por , pois será as coordenadas do vértice +p na coordenada y, o foco então é:
Passo 5
E por final, a letra (d) pede a equação da diretriz, a equação geral da diretriz é:
Substituindo pelos valores que calculamos antes: