Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.5 - Ex. 47

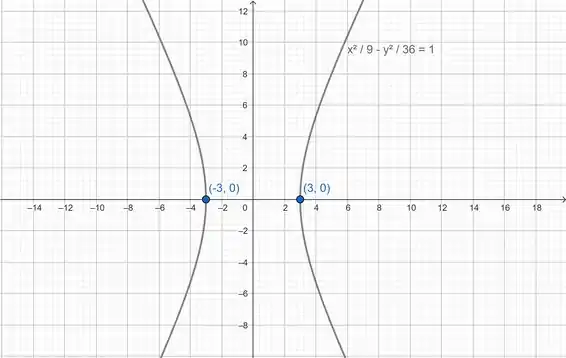
Encontre uma equação para a cônica que satisfaz as condições dadas

47. Hipérbole, vértices ± 3,0 , assíntotas y = ± 2 x

Passo 1

Nessa questão, nos foi dado o nome da cônica, seus vértices e assíntotas para encontrarmos sua equação.

Temos a hipérbole com focos em 2,0 e 2,8 . Além disso, deveremos ter assíntotas:

y = ± 2 x

E vértices em:

± 3,0

Bom, sabemos que é uma hipérbole, e hipérboles tem equações no formato

x - x 0 2 a 2 - y - y 0 2 b 2 = 1  

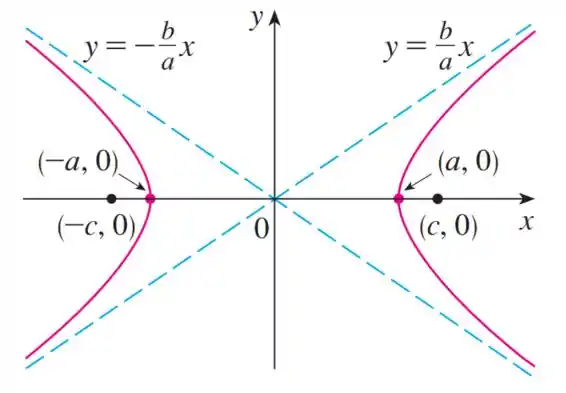
ou

y - y 0 2 a 2 - x - x 0 2 b 2 = 1

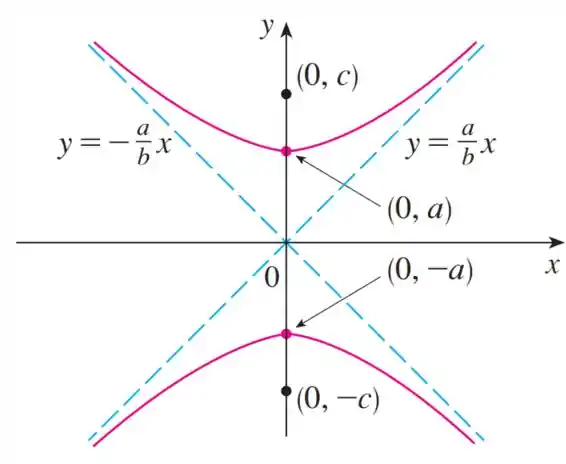
dependendo qual seu eixo.

Note que essa é uma hipérbole com eixo maior no eixo Y , podemos ver isso pelas coordenadas do vértice, que mudam apenas em x , então a equação é do tipo

x - x 0 2 a 2 - y - y 0 2 b 2 = 1

O centro da hipérbole fica na metade do caminho entre seus vértices, como aqui temos

V 1 = - 3,0   e   V 2 = ( 3,0 )

nosso centro será 0,0 . Portanto

( x 0 , y 0 ) = ( 0,0 )

Os vértices são V = ( x 0 ± a , y 0 ) , então sabemos que a = 3

Passo 2

Sabemos que as assíntotas de uma hipérbole com eixo maior em X são y = ± b a x ,

então

b = 2 a

b = 6

Com isso tudo, podemos montar nossa equação:

x - x 0 2 a 2 - y - y 0 2 b 2 = 1

x 2 9 - y 2 36 = 1

Resposta

x 2 9 - y 2 36 = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre uma equação da parábola. A seguir, ache o foco e a diretriz.
Encontre o vértice, o foco e a diretriz da parábola e esboce seu gráfico. 2 x = - y 2
Encontre os vértices e os focos da elipse e esboce seu gráfico. x 2 9 + y 2 5 = 1
1-8. Encontre o vértice, o foco e a diretriz da parábola e esboce seu gráfico.1. x 2 = 6 y
31-48. Encontre uma equação para a cônica que satisfaz as condições dadas.35. Parábola, vértice ( 2,3 ) , eixo vertical, passando em ( 1,5 )