Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.5 - Ex. 38
Encontre uma equação para a cônica que satisfaz as condições dadas
Elipse, Focos vértices
Passo 1
Opa, tudo tranquilo? Questãozinha sobre elipse aqui, vamos lá!
Aqui a gente quer encontrar uma equação pra uma elipse com focos e vértices . Para ajudar a visualizar a questão a gente pode tentar desenhar um esboço dessa elipse com esses dados:
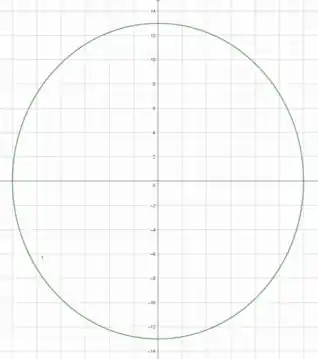
Note que essa é uma elipse com eixo maior no eixo , podemos ver isso pelas coordenadas do vértice, que mudam apenas em .
Pra isso vamos lembrar que elipses tem equações no formato:
MAS, PORÉM, CONTUDO, TODAVIA, ENTRETANTO... Essa equação só é verdade para elipses com o eixo maior na HORIZONTAL! Veja que no nosso caso, os vértices dessa elipse estão no eixo Y. Para corrigir isso, basta fazermos a seguinte alteração:
Só precisamos agora identificar essas variáveis e substituir na equação geral!
Passo 2
O par é o centro da elipse, e sabemos que o centro da elipse fica na metade do caminho entre seus vértices. Então, como aqui temos , nosso centro será . Portanto
Além disso:
é a distância do centro da elipse até um dos vértices, nesse caso
é a distância do centro da elipse até um dos “vértices” do eixo menor, que ainda não sabemos
E por fim, é a distância do centro da elipse ao foco, então teremos
E, para matar a charada de vez, sabemos que existe uma relação entre , tal que
então trocando os valores, encontramos:
Com isso tudo, podemos montar nossa equação: