Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 42
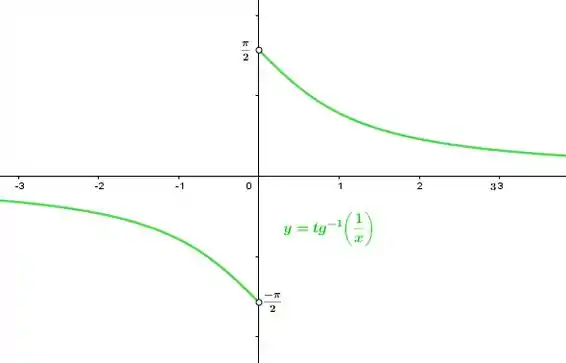
Faça o gráfico da curva
Passo 1
Inicialmente vamos considerar e observar o que essa função tem a nos “dizer”.
Observe que o domínio de corresponde ao conjunto dos números Reais. Como o temos uma composição de funções cujo argumento é igual a que é uma função que não é definida para teremos que o domínio de corresponde, corresponde a todos os números reais, exceto .
Sendo assim, o gráfico de é definida para todo.
Passo 2
Em seguida verificaremos, se possui raízes, ou seja, se o gráfico toca o eixo No entanto se nos lembrarmos bem, a função só corta toca o eixo em , porém, esse ponto não pertence ao domínio da Sendo assim, não toca o eixo
Passo 3
Determinaremos agora e , para em seguida verificarmos se possui máximos, mínimos ou pontos de inflexão. Dessa maneira temos que,
Pela regra da cadeia teremos,
Calculando a segunda derivada utilizando a regra do quociente,
Passo 4
Vamos agora identificar se possui pontos críticos
Em relação aos pontos de críticos temos que
Porém não pertence ao domínio de , e consequentemente não pode ser um ponto de m máximo ou um mínimo.
Passo 5
Vamos agora identificar se possui pontos de inflexão
Em relação aos pontos de inflexão temos que
Sendo assim temos um candidato a ponto de inflexão, vamos verificar se há mudança de sinal nas proximidades de cada um deles.
Perceba que, para valores dentro do intervalo , assume valores negativos (tem concavidade para baixo). E para valores dentro do intervalo , irá assumir valores negativos ( tem concavidade para baixo). Logo, não é um ponto de inflexão no intervalo de ou seja, não possui mudança de concavidade nesse ponto.
Já, para valores dentro do intervalo , assume valores positivos (tem concavidade para cima). E para valores dentro do intervalo , irá assumir valores positivos ( tem concavidade para cima). Logo, não é um ponto de inflexão no intervalo de ou seja, não possui mudança de concavidade nesse ponto.
Passo 6
Para finalizar verificaremos se possui assíntotas verticais ou horizontais.
No que se refere as assíntotas horizontais temos que
Logo, possui uma assíntota horizontal em .
No que se refere as assíntotas verticais, não há nenhum ponto no domínio de que faça com que
Resposta
