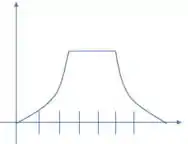
8. A figura a seguir mostra o gráfico posição versus tempo para um elevador que sobe entre uma parada e outra.
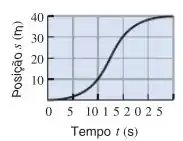
a) Estime a velocidade do elevador no meio da subida.
b) Faça um esboço dos gráficos das curvas velocidade versus tempo e aceleração versus tempo.
Passo 1
a) Então pessoal, para estimarmos a velocidade do elevador no meio da subida basta pegarmos os dois intervalos de tempo associados a este “meio” e utilizar a notação de velocidade média, que é:
O meio está entre e , cujas posições estão, respectivamente, em e , logo:
E essa é a nossa velocidade!
Passo 2
b) Antes de esboçarmos os gráficos de velocidade e aceleração, vale lembrar que a derivada da posição resulta na velocidade e a derivada da velocidade resulta na aceleração. Sendo assim, temos que analisar a derivada primeira e a derivada segunda da função!
Para a velocidade, se observarmos bem o gráfico notaremos que o mesmo começa crescente, fica um tempo constante e depois aparenta começar a cair de novo. Com esses dados em mente, um esboço possível da velocidade seria:
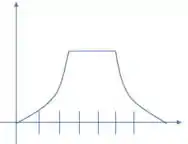
Passo 3
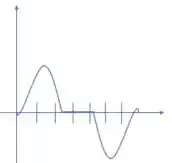
Para a aceleração temos que analisar quanto as concavidades do gráfico que nos foi dado, ok? Começamos com uma concavidade positiva, ou seja, uma aceleração positiva. Em seguida temos um ponto de inflexão e a concavidade muda de sentido ficando constante por um tempo. Por fim essa mesma situação se repete, mas com sentidos invertidos. Dessa forma, um possível esboço da aceleração seria:
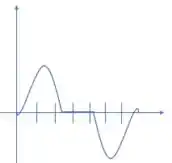
E essa é a nossa resolução, galera!
Resposta
a)
b) Velocidade versus tempo:
Aceleração versus tempo: