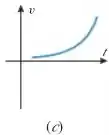
2. Abaixo estão os gráficos de três funções velocidade. Em cada caso, determine o sinal da aceleração e, então, se a partícula está aumentando ou diminuindo a velocidade.

Antes de analisarmos a aceleração a partir da função dada, temos que lembrar o seguinte, galera: a derivada da função velocidade resulta na função aceleração, ok? Então o que temos que fazer é analisar a derivada da função através da curva dada, beleza? Então bora lá!

Se observarmos com calma o gráfico que nos foi dado, temos que a derivada é positiva e se mantém positiva. Dessa forma, podemos concluir que o sinal da aceleração é positivo.

Além disso, temos que a velocidade da partícula aumenta à medida que o tempo passa, então podemos dizer que a velocidade está aumentando!

E essa é a nossa análise da curva em questão, gente!