Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.6 - Ex. 4
4. Para os gráficos a seguir, associe as funções posição (a)–(c) com as funções velocidade (I)–(III) correspondentes.
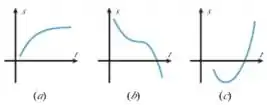
Passo 1
Então pessoal, antes de fazermos a análise e associação dos gráficos temos que lembrar o seguinte: a derivada da função posição resulta na função velocidade, então o que devemos fazer é analisar a derivada da função posição e associar ao gráfico correto, beleza? Então bora lá!
Para a curva a) temos que a derivada é positiva em todo o intervalo, até o momento em que a derivada vai se aproximando de zero, ou seja, a partícula para. Sendo assim, podemos associar o gráfico de a) ao gráfico (III), pois nesse gráfico a velocidade vai diminuindo até chegar a zero, como queremos!
Passo 2
Para a curva b) temos que a derivada começa negativa, apresenta um ponto crítico em um certo valor de e depois continua negativa. Sendo assim, podemos associar o gráfico de b) ao gráfico (I), pois nesse gráfico a velocidade inicialmente é negativa, vira zero em um momento e depois começa a aumentar negativamente de novo, assim como no gráfico b). Sem dúvidas formam um par!
Passo 3
Por fim, para a curva c) temos que o gráfico associado é o (II), por princípio de exclusão.
E estão aí nossas associações, pessoal!
Resposta
a) está associado a (III);
b) está associado a (I);
c) está associado a (II).