Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 17
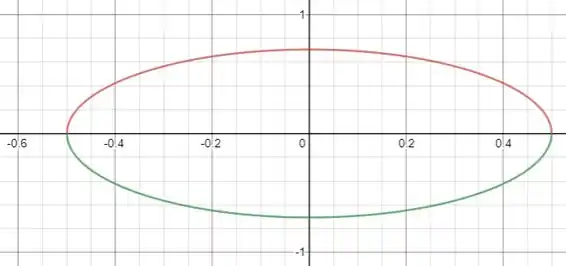
Faça o gráfico da elipse por meio dos gráficos das funções que são a metade superior e inferior da elipse.
Passo 1
Olá, meu amigo, Yuri aqui e agora eu e você iremos resolver esta atividade.
A questão pede para fazermos o gráfico da elipse obtendo duas funções que representam as metades inferior e superior da elipse. Para isso, teremos que encontrar quem são as equações que representam a parte inferior e a parte superior da nossa elipse.
Podemos fazer isso isolando a variável da equação da elipse que nos foi dada, teremos assim duas equações em função de .
Passo 2
Dito isso, o primeiro passo é passar todo mundo que não é para o outro lado da igualdade.
Tirando a raiz quadrada em ambos os lados e lembrando que , temos:
Agora que temos duas equações, cada uma sendo uma parte da elipse, agora podemos criar os dois gráficos.
Passo 3
Para construir o gráfico, precisamos de alguns pontos. Precisamos das raízes das nossas equações e precisamos dos seus vértices. Para encontrarmos as raízes iremos igualar nossa equação a zero:
Agora, para entendermos melhor a localização da "cabeça" da nossa elipse, chamada de vértice, precisamos encontrar onde a elipse atinge o ponto mais alto ou mais baixo. Para fazer isso, calculamos o valor de no vértice da equação. Isso é como encontrar o meio exato da elipse.
Depois, uma vez que temos esse valor de , o substituímos de volta na equação para descobrir a altura da elipse nesse ponto, que é o valor de no vértice.
Para as nossas equações
A coordenada do vértice é determinada quando a parte dentro da raiz quadrada atinge seu valor mínimo, que ocorre quando . Substituindo na equação, obtemos:
Com esses pontos em mãos, então desenhar o gráfico das nossas equações.
Passo 4
Com ajuda do GeoGebra, irei desenhar esse gráfico. Em vermelho temos a parte superior (sinal de ) e em verde a parte inferior (sinal de ):
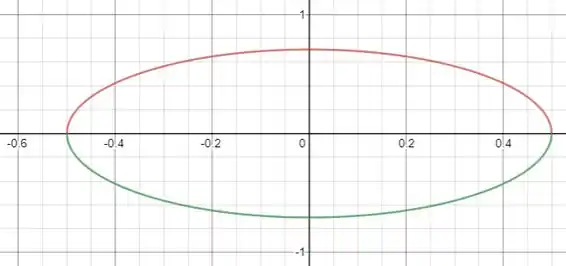
Resposta
