Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 25
Use os gráficos para determinar qual das funções e é, eventualmente, maior (isto é, maior quando for muito grande).
Passo 1
Falaii galerinha do RA, bora para mais umazinhaaa??
Para resolver essa questão vamos utilizar a teoria de James Stewart, podemos analisar o comportamento das funções e à medida que se torna muito grande. Isso pode ser feito observando o crescimento relativo das funções e comparando-as.
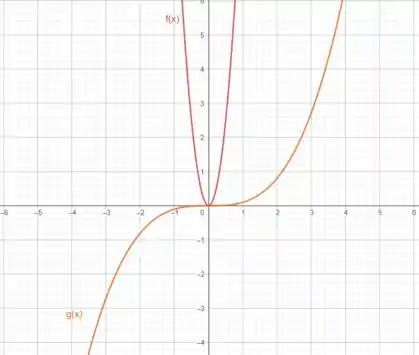
Primeiro, vamos traçar os gráficos das duas funções para visualizar seu comportamento:
- Esta é uma função quadrática, que possui um formato de "parábola" que se abre para cima.
- : Esta é uma função cúbica, que possui um formato de "curva" que aumenta de forma mais acentuada que uma parábola conforme aumenta.
Passo 2
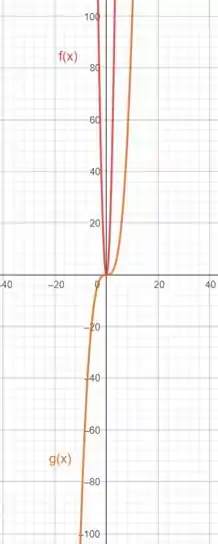
Agora, ao observar os gráficos, podemos notar que a função cúbica cresce mais rapidamente do que a função quadrática conforme se torna muito grande.
Isso acontece porque, para valores de muito grandes, o termo na função domina sobre o termo no denominador, enquanto na função o termo cresce mais lentamente do que
Portanto, concluímos que é eventualmente maior que quando é muito grande.
A seguir plotamos as duas curvas:
Resposta
Portanto, concluímos que é eventualmente maior que quando é muito grande.