Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 23

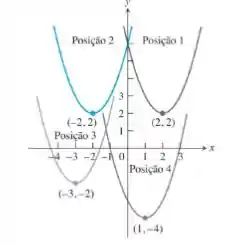
Associe as equações listadas nos itens a - ( d ) aos gráficos da figura seguinte.

  1. y = x - 1 2 - 4
  2. y = x - 2 2 + 2
  3. y = x + 2 2 + 2
  4. y = x + 3 2 - 2

Passo 1

Esta questão pode parecer complicada, visto que temos que reconhecer o gráfico de quatro equações. Entretanto, no final, ela não passa de mais uma questão simples. Para resolvê-la, basta termos dois conhecimentos: o gráfico de uma função f x = x 2 e como uma translação horizontal e uma vertical afeta o seu gráfico.

Vamos agora relembrar o que acontece quando fazemos uma translação horizontal. Para obter uma curva g ( x ) a partir da f ( x ) , fazemos:

g x = f x + h = x + h 2

Quando h > 0 , a translação será para a esquerda. Quando h < 0 , a translação será para a direita.

Já para fazermos uma translação vertical, fazemos a seguinte relação:

g x = f x + k

Quando k > 0 , a translação é para cima. Quando k < 0 , a translação é para baixo.

Portanto, vamos relacionar as translações dos gráficos com as equações dadas.

Passo 2

Vamos começar pela posição 1. O vértice da parábola se encontra no ponto ( 2,2 ) . Portanto, comparado ao vértice da parábola f x = x 2 , o qual está no ponto O = ( 0,0 ) , esta curva foi transladada para a direita em 2 unidades ( h = - 2 ) e para cima em 2 unidades ( k = 2 ) . Portanto, temos:

y = x - 2 2 + 2

Equação da letra b )

Passo 3

Na posição 2, o vértice da parábola se encontra no ponto ( - 2,2 ) . Portanto, comparado ao vértice da parábola f x = x 2 , o qual está no ponto O = ( 0,0 ) , esta curva foi transladada para a esquerda em 2 unidades ( h = 2 ) e para cima em 2 unidades ( k = 2 ) . Portanto, temos:

y = x + 2 2 + 2

Equação da letra c )

Passo 4

Na posição 3, o vértice da parábola se encontra no ponto ( - 3 , - 2 ) . Portanto, comparado ao vértice da parábola f x = x 2 , o qual está no ponto O = ( 0,0 ) , esta curva foi transladada para a esquerda em 3 unidades ( h = 3 ) e para baixo em 2 unidades ( k = - 22 ) . Portanto, temos:

y = x + 3 2 - 2

Equação da letra d )

Passo 5

Na posição 4, o vértice da parábola se encontra no ponto ( - 2,2 ) . Portanto, comparado ao vértice da parábola f x = x 2 , o qual está no ponto O = ( 0,0 ) , esta curva foi transladada para a direita em 1 unidade ( h = - 1 ) e para baixo em 4 unidades ( k = - 4 ) . Portanto, temos:

y = x - 1 2 + 4

Equação da letra a )

Resposta

Posição 1 – equação b )

Posição 2 – equação c )

Posição 3 – equação d )

Posição 4 – equação a )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Neste exercício, consideramos a família de funções f x = x n , onde n é um inteiro positivo.a) Faça os gráficos das funções y = x , y = x 4 e y = x 6 , na mesma tela usando a janela retangular [ - 1 ,
Neste exercício, consideramos a família de funções f x = 1 / x n , onde n é um inteiro positivo.a) Faça o gráfico das funções y = 1 / x e y = 1 / x 3 , na mesma tela usando a janela retangular [ - 3 ,
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função. f x = s e n 2 ( 1000 x )
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função. f x = x x 2 + 100
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função. f x = x 3 - 225 x