Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 15
Faça o gráfico da elipse por meio dos gráficos das funções que são a metade superior e inferior da elipse.
Passo 1
A questão pede para fazermos o gráfico da elipse obtendo duas funções que representam as metades inferior e superior da elipse.
Você deve estar se perguntando, por que vamos obter duas funções para representar a elipse...
O que ocorre é que quando isolarmos o na equação , vamos obter o seguinte:
E agora é só tirar a raíz dos dois lados, certo?
Errado!
Além de tirar a raíz, você tem que considerar que pode ser negativo ou positivo, ou seja:
Daí, você pode agora obter uma equação que representa a parte superior (usando o sinal positivo) e outra que representa a parte inferior (usando o sinal negativo).
Passo 2
Dessa forma, temos para a parte superior da elipse que:
E para a parte inferior que:
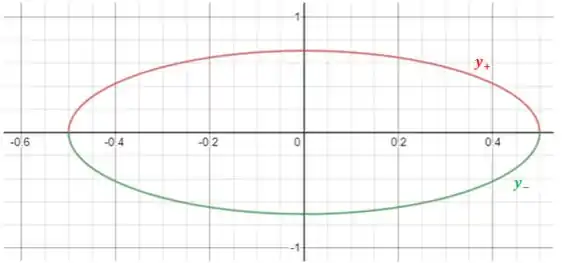
Por fim, basta desenhar a sua elipse. Para isso, vamos encontrar alguns pontos de interesse.
Passo 3
Aqui é interessante, você saber os pontos em que sua função irá cortar o eixo e o eixo .
Usando
Precisamos que:
Portanto,
Portanto, ela corta o eixo em .
Fazendo o mesmo para a parte negativa, você vai encontrar que ela corta o eixo em .
Passo 4
Agora, vamos encontrar onde ela corta o eixo , para isso vamos fazer que .
E na parte inferior você vai encontrar que:
Ou seja, nossa elipse corta o eixo em e e corta o eixo em e
Desenhando o gráfico dessa elipse obtemos:
Resposta
Esboço de gráficos.