Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 30
Faça o gráfico da função para vários valores de . Descreva como a variação de afeta o gráfico.
Passo 1
E aí, galerinha!
O problema pede para estudarmos o gráfico de conforme varia.
Primeiro vamos analisar o domínio da função, pois assim poderemos descobrir quais são os valores possíveis para e para .
Por termos aqui uma raiz, não podemos ter valores negativos dentro dela.
Depois iremos analisar diversar entradas para o valor de e plotarmos no GeoGebra ou Desmos, veja que você pode fazer esse gráfico na mão, utilizando uma tabela, onde plota diferentes valores para e e recebe os valores de , da um pouco de trabalho plotar tantos pontos mas é uma opção.
Passo 2
Para ser definida, o conteúdo dentro da raiz deve ser maior ou igual a , ou seja:
Assim, se , , de modo que o domínio de será real. Por outro lado, se , o domínio não será toda a reta real, ele será restrito!
Bora começar!
Passo 3
Primeiro vamos fazer os plots para :
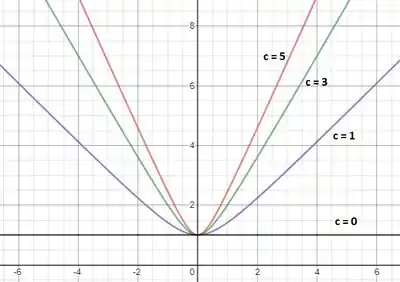
Conforme cresce, a curva vai se fechando, porém todas passam pelo ponto .
Essas curvas são ramos de hipérboles.
Tranquilo até aqui?
Passo 4
Agora vamos ver o que acontece para :
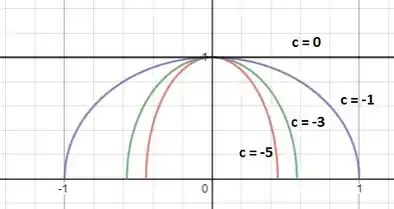
Agora as curvas vao se fechando também, porém para baixo de !
Agora as curvas são arcos de elipse!
Entendeu tudo? Responde Aí!
Resposta
Esboço de gráfico.