Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.1 - Ex. 6
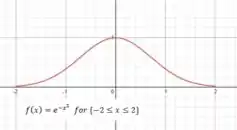
(a) Faça o gráfico da função .
(b) Estime a área sob o gráfico de usando quatro retângulos aproximantes e tomando como pontos amostrais (i) as extremidades direitas e (ii) os pontos médios. Em cada caso, esboce a curva e os retângulos.
(c) Aperfeiçoe suas estimativas da parte (b) usando oito retângulos.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Nessa questão temos a função
E primeiro iremos fazer o gráfico dessa função. Como essa não é uma função conhecida e não conseguimos obtê-la com operações gráficas, irei usar um software gráfico para fazer o gráfico. Aqui usarei o GeoGebra.
Após isso, iremos utilizar de retângulos abaixo do gráfico para que possamos realizar uma aproximação da sua área.
Esses retângulos serão formados a partir das extremidades direitas de cada intervalo e a partir dos pontos médios de cada intervalo.
Usarei para a letra b) um total de quatro intervalos e para a letra c) um total de oito intervalos.
Lembrando que a área de um retângulo é dado como:
Onde a base nesse caso será a variação em e a altura será o valor da função calculado no ponto da extremidade direita do intervalo ou do ponto do ponto médio do intervalo.
Passo 2
Obtendo o gráfico a partir do GeoGebra: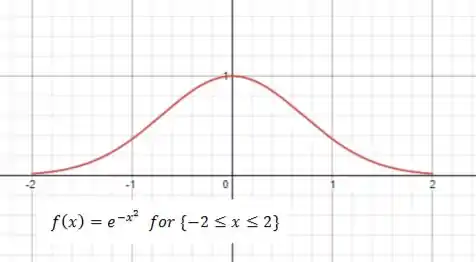 
Passo 3
Para utilizarmos a aproximação pela extremidade direita, iremos criar nossos retângulos e iremos utilizar como na função a extremidade direta do retângulo.
Temos
e
, logo cada retângulo terá uma área igual a .
Graficamente o que teremos é:
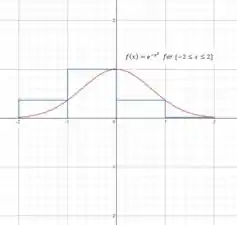
A área de cada retângulo é dada por
Como temos 4 retângulos temos então:
Onde é a ‘altura’ do nosso retângulo e é a base.
Dessa forma, teremos:
Passo 4
Agora a situação do ponto médio, iremos utilizar como nosso em o ponto médio entre os dois pontos que compõem os lados do nosso retângulo.
O número de retângulos e a base de cada retângulo continua sendo igual ao do passo anterior.
Graficamente o que temos é:
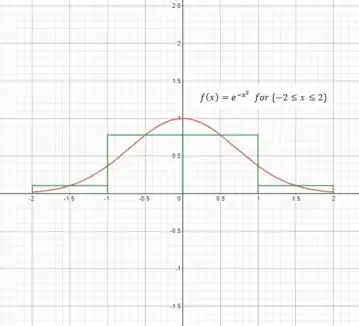
Calculando teremos:
No entanto, agora o valor de é o ponto médio de cada intervalo, portanto:
Passo 5
Aqui iremos apenas aumentar a quantidade de retângulos que temos, consequentemente iremos recalcular a base, desses triângulos.
Temos
e
, logo:
Esboçando o gráfico:
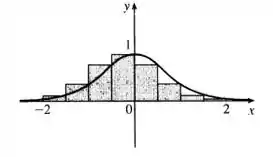
Passo 6
Usando agora o ponto médio teremos para o gráfico da função o seguinte:
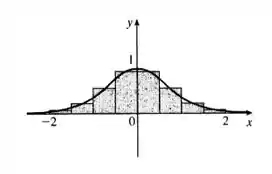
Por conta da simetria da figura, nós vemos que podemos calcular apenas a porção de positivo e multiplicar por para obter a porção com negativo, logo:
