Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.2 - Ex. 6
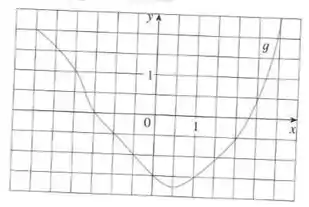
O gráfico de é apresentado. Estime com seis subintervalos usando (a) extremidades direitas, (b) extremidades esquerdas e (c) pontos médios.
Passo 1
E aí! tudo certinho?
Nesse problema temos que estimar a integral da função de até cujo gráfico é dado por
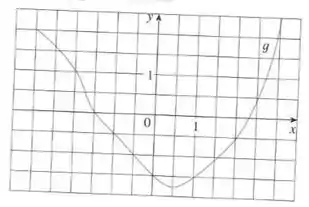
Pra isso temos que determinar quatro subintervalos com (a) extremidades direitas, (b) extremidades esquerdas e (c) pontos médios.
Basicamente o que vamos resolver aqui portanto é uma soma de Riemann.
A soma de Riemann para uma função com subintervalos pode ser definida pelo seguinte somatório:
Ela representa a soma das áreas de retângulos que são obtidos a partir da função.
A ideia é basicamente dividir o intervalo em subintervalos igualmente espaçados.
Esses serão as bases dos retângulos.
Para a altura do retângulo, pega-se o valor da função em um ponto dentro do subintervalo .
E aí há três opções.
Escolher um valor da função calculado no do extremo esquerdo do subintervalo , do meio do subintervalo () ou do extremo direito do subintervalo ).
Passo 2
Determinando o delta desse exercício:
Vamos agora estimar a soma usando valores de das extremidades direitas dos subintervalos de comprimento que variam de até :
Estimando com extremidades direitas:
Agora basta procurar por esses valores no gráfico:
Passo 3
Estimando com extremidades esquerdas, para isso vamos olhar para os valores do extremo esquerdo dos subintervalos de comprimento que variam de até :
Dessa forma teremos:
E procurando por esses valores no gráfico, ficamos com:
Passo 4
Estimando com pontos médios, agora vamos olhar para os valores médios dos subintervalos de comprimento que variam de até :
De forma que teremos:
E aí! Entendeu tudo? Responde Aí!
