Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 59
Faça o gráfico da função
E explique por que ela é injetora. Use então um sistema de computação algébrica (SCA) para encontrar uma expressão explícita para . (Seu SCA vai produzir três expressões possíveis. Explique por que duas delas são irrelevantes neste contexto.)
Passo 1
Fala aí, pessoal. Tudo belezinha.
Bom, essa questão deu pra gente a função
E pediu pra gente plotar seu gráfico e explicar o porque de ela ser injetora.
Além disso ele pede pra gente fazer isso usando o sistema de computação algébrica (SCA) para encontrar uma expressão explícita para , que irá gerar três expressões possíveis, sendo duas delas irrelevantes, e nós também teremos que explicar o porque disso acontecer.
Vamos então plotar esse gráfico e analisar essas informações.
Passo 2
Para esta solução, usaremos o SCA chamado Derive.
Para usar o Derive, precisamos escrever a função da seguinte maneira
Repare que aqui trocamos o por .
Então plotando o gráfico no software, ficamos com
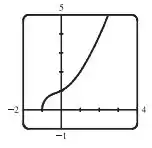
Pelo gráfico, podemos ver que a função é injetora, pois cada valor de possui um único valor de .
uma função injetora é uma função que preserva a distinção: nunca aponta elementos distintos de seu domínio para o mesmo elemento de seu contradomínio. Em outras palavras, cada elemento do contradomínio da função é a imagem de no máximo um elemento de seu domínio.
Isso também pode ser entendido traçando retas horizontais e observando que elas interceptam o gráfico da função uma única vez.
Passo 3
Agora, podemos encontrar pelo programa uma expressão para que será a seguinte
Onde
O software nos dá 3 soluções, porém duas envolvem números complexos, então somente esta é relevante.
Resposta
Onde