Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.3 - Ex. 9
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção 1.2, e então aplicando as transformações apropriadas.
Passo 1
Eaee, belezinha?? Bom... a questão quer que esbocemos o gráfico da seguinte função:
Para isso, a questão quer que utilizemos gráficos de uma das funções básicas dadas na seção 1.2.
Assim, a função da seção 1.2 que mais parece com essa é a :
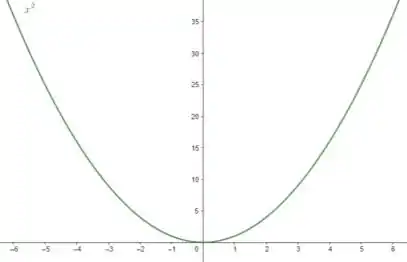
Bom pessoal, esta função é do tipo parabólica, com raiz única igual a .
Agora que temos essa função, vamos descobrir como desenhamos 😉
Passo 2
Perceba que a única diferença entre e é esse sinal negativo.
Nesta seção 1.3, aprendemos que quando temos o negativo de uma função devemos espelhá-la em relação ao eixo do gráfico. Isso porque, graças ao sinal de menos, tudo que é positivo vai ficar negativo e tudo que é negativo vai ficar positivo!
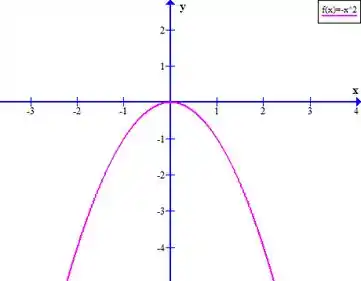
Assim, espelhando , obtemos o gráfico de :
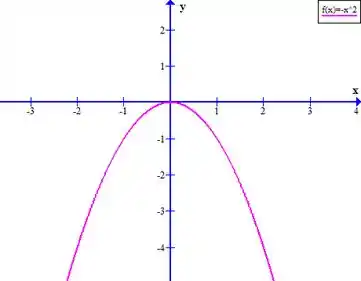
Entendeu direitinho?? Responde aee 😉
Resposta
