Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.3 - Ex. 14
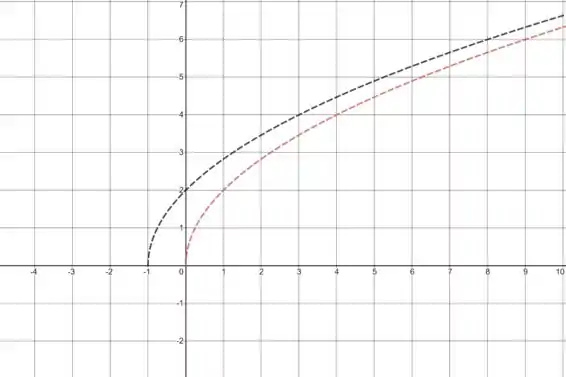
Faça o gráfico da função à mão, não usando pontos, mas a partir dos gráficos de uma das funções padrão dadas na seção 1.2, e então aplique as transformações apropriadas.
Passo 1
Olá, meu brother. Vamos para mais uma resolução?
Veja bem, a gente tem a função:
E a partir do gráfico de uma função mais simples, iremos construir o gráfico da função dada. Para isso, vamos utilizar nossos conhecimentos de como as constantes afetam o comportamento de um gráfico.
Bom pessoal, esta função é do tipo raiz. Então vamos utilizar como base o gráfico da função:
Passo 2
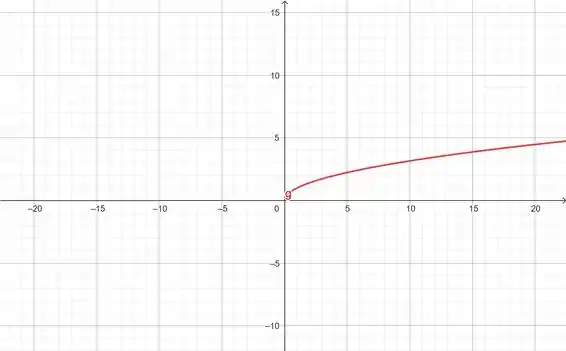
Vamos começar com o gráfico da função padrão/pai
O gráfico de é obtido esticando verticalmente o gráfico de por um fator de .
Portanto, se esticarmos verticalmente o gráfico de por um fator de , obteremos o gráfico de .
No gráfico abaixo:
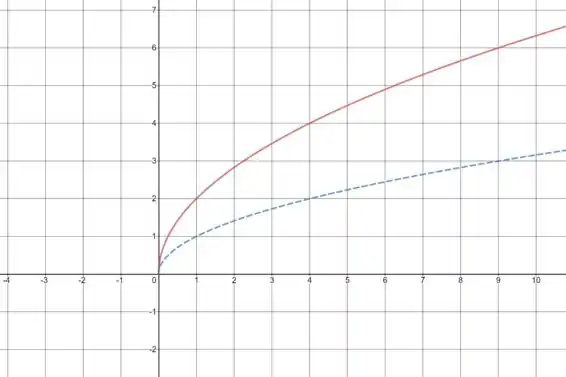
A curva tracejada azul representa .
A curva sólida vermelha representa .
Quando deslocamos o gráfico de por unidades para a esquerda, obtemos o gráfico de .
Portanto, o gráfico de é obtido deslocando o gráfico de por 1 unidade na direção da esquerda.
No gráfico abaixo:
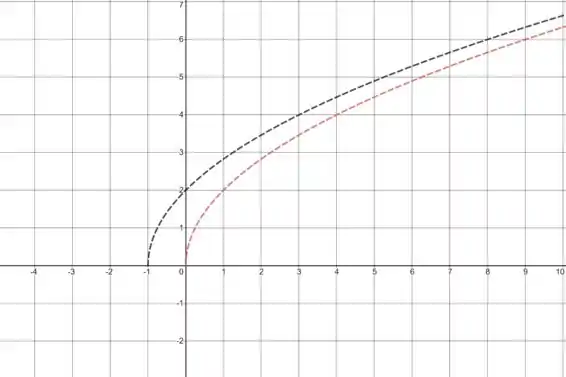
A curva tracejada vermelha representa .
A curva sólida preta representa .
Resposta
