Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.3 - Ex. 19
Faça o gráfico da funç��o à mão, não usando pontos, mas a partir dos gráficos de uma das funções padrão dadas na seção 1.2, e então aplique as transformações apropriadas.
Passo 1
Olá! Como você está? Vamos resolver mais uma atividade juntos, tenha confiança que tudo dará certo.
Veja só, agora precisamos criar o gráfico da função
usando o gráfico de uma função padrão da seção 1.2. O que isso quer dizer? Simplesmente que precisamos lembrar como as constantes afetam o comportamento do gráfico, analisar e comparar a função do gráfico padrão com a nossa função. É desse processo que obteremos nosso resultado. Vamos lá!
O gráfico base será o seguinte:
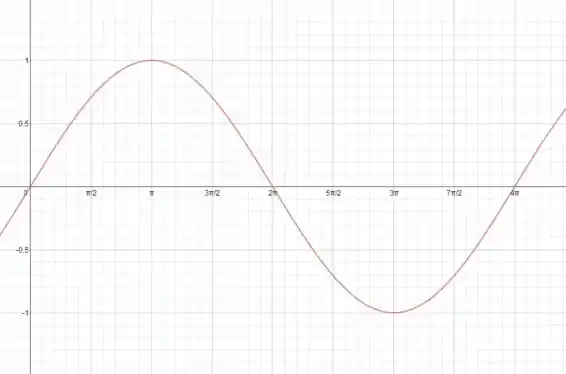
Esse é o gráfico da função:
E servirá como base para a gente.
Passo 2
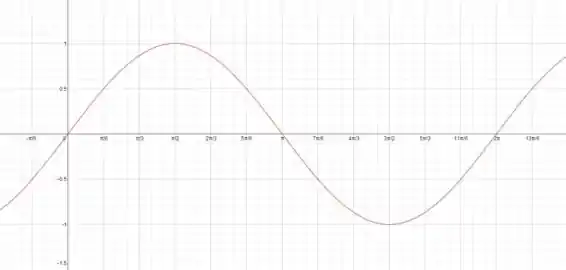
Bom pessoal, esta função é do tipo trigonométrica. Porém, temos aqui um coeficiente de dentro do , multiplicando o .
Aprendemos que quando temos uma função do tipo , devemos “alargar” a função. Melhor dizendo, as oscilações devem ficar mais longas. Como está sendo dividido pela metade, as ondas serão alongadas pelo dobro.
Temos:
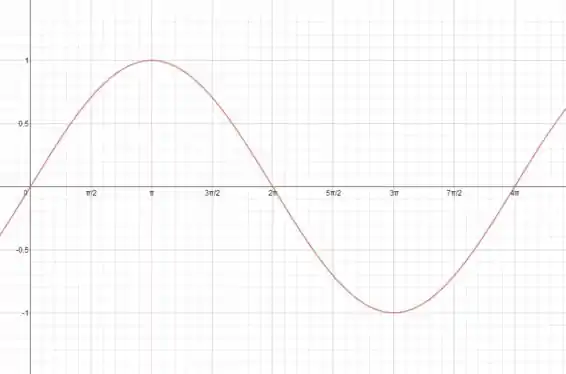
Eu fiz aqui o gráfico utilizando o GeoGebra, para melhor visualização, mas o mais importante aqui é você entender o como o gráfico é afetado pelas constantes.
Resposta
