Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 49
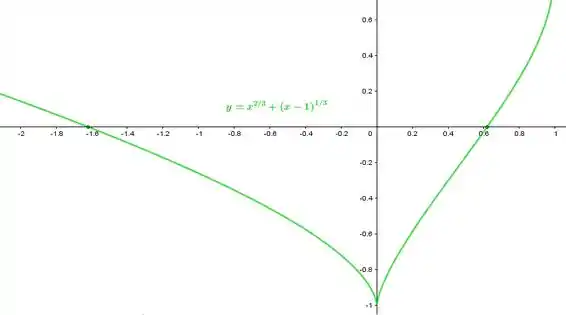
Faça o gráfico da função . Em seguida, use a primeira derivada da função para explicar o que você está vendo.
Passo 1
Inicialmente vamos considerar em seguida, manualmente ou com auxílio de algum software obteremos um gráfico parecido com o que está abaixo,
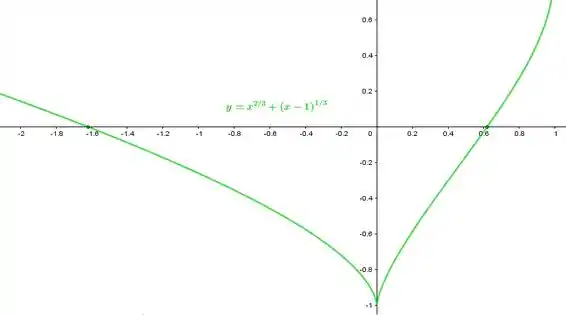
Passo 2
Agora, explicaremos o por que o gráfico ficou daquela forma, mas para isso precisaremos sabe qual a cara de ou seja,
Utilizando a regra da soma e a regra da cadeia teremos
Reescrevendo as potências teremos,
Sendo assim,
Passo 3
Sabemos que através de podemos encontrar pontos críticos e isso irá nos ajudar a explicar o que está acontecendo com o gráfico de . Dessa maneira, para encontrar pontos críticos precisamos que ,isto é,
Dividindo a igualdade por temos
Para que a fração seja igual a zero,precisamos que o numerador seja igual a zero, ou seja,
Pela propriedade de potência de potência
Aplicando a fórmula de Baskara veremos que esse polinômio não possui raízes reais.
Dessa forma, não encontramos nenhum valor para no domínio de , que faça com que . Logo não possui pontos críticos em seu domínio, consequentemente, não irá possuir nem pontos de máximo nem pontos de mínimo, como pudemos comprovar ao ver o gráfico da função.
Além disso, vamos analisar como se comporta nos intervalos e . Dessa maneira, temos que no intervalo ou seja, decrescente . Já no intervalo de ou seja, é crescente.
Resposta
Como não foi encontrado nenhum valor para no domínio de , de maneira que . Concluímos que não possui pontos críticos em seu domínio e consequentemente, não irá possuir nem pontos de máximo nem pontos de mínimo . Além disso, apresenta um comportamento crescente no intervalo de e decrescente no intervalo de por isso o gráfico se apresenta dessa maneira:
