Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 32
Faça o gráfico da função para vários valores de . Descreva como a variação de afeta o gráfico.
Passo 1
Fala aí, tudo belezinha.
Bom, esse problema pede para estudarmos o gráfico de para vários valores de e descrever como essa variação de afeta o gráfico da função.
Então faremos isso! Vamos supor diferente valores para e plotar os gráficos das funções que obtivermos.
Mas aqui a primeira coisa que precisaremos ter em mente é que essa é função possui uma expressão dentro de uma raiz quadrada, e isso fará com que ela não esteja definida para todos os valores de dependendo de qual seja o valor de , já que raízes de índice par não admitem radicando negativo.
Então também precisaremos estudar as condições de domínio da função.
Mas vem comigo que te ajudo com isso no passo a passo.
Passo 2
Primeiro vamos analisar o domínio da função. Perceba que sendo
Então precisamos ter
Assim:
Assim, se , , de modo que o domínio de será real.
Por outro lado, se , o domínio não será toda a reta real, ele será restrito!
Sendo assim, vamos dividir nosso problema nessas duas condições.
Passo 3
Primeiro vamos fazer os plots para :
Se a função será:
Se a função será:
Se a função será:
Perceba que conforme cresce, a curva vai se fechando, porém todas passam pelo ponto . Essas curvas são ramos de hipérboles. Veja:
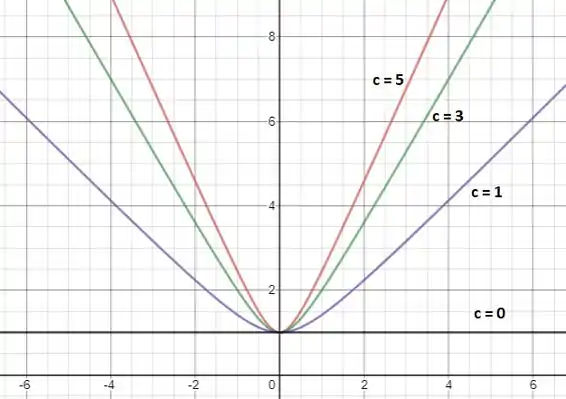
Passo 4
Agora vamos ver o que acontece para :
Se a função será:
Se a função será:
Se a função será:
Perceba que conforme vai ficando mais negativo, a curva vai se fechando, porém todas também passam pelo ponto . Essas curvas são ramos de arcos de elipse. Veja:
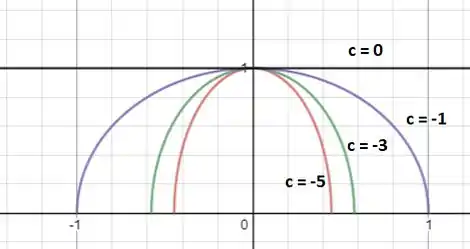
Agora as curvas são arcos de elipse!
Resposta
Quando é positivo, temos gráficos hiperbólicos e a medida que cresce, a curva vai se fechando, porém todas passam pelo ponto .
Quando é negativo, temos gráficos elípticos, e a medida que diminui a curva vai se fechando, porém todas também passam pelo ponto .