Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 18
Faça o gráfico da hipérbole por meio dos gráficos das funções que são os ramos superior e inferior da hipérbole.
Passo 1
Falaii galerinha do RA, bora resolver essa juntinho?
Simboraa
Para resolver essa questão utilizando a teoria de James Stewart, podemos começar observando a equação da hipérbole dada:
Primeiro, reescrevemos a equação na forma padrão de uma hipérbole:
Comparando com a forma padrão:
Podemos identificar que .
Isso significa que
Passo 2
Agora, sabemos que o gráfico da hipérbole terá dois ramos: um superior e um inferior. Para desenhar esses ramos, precisamos traçar as funções correspondentes a cada ramo.
A equação geral da hipérbole é
onde é a distância do centro ao vértice no eixo é a distância do centro ao vértice no eixo .
Para o ramo superior, usamos a função:
Para o ramo inferior, usamos a função:
Agora, podemos plotar essas funções nos eixos cartesianos. No entanto, é importante notar que a hipérbole está centrada na origem (0,0) e possui um eixo de simetria ao longo do eixo y.
Passo 3
Minha F(x) representa a parte positiva do nosso gráfico, e minha G(x), resepresenta a parte negativa do nosso gráfico.
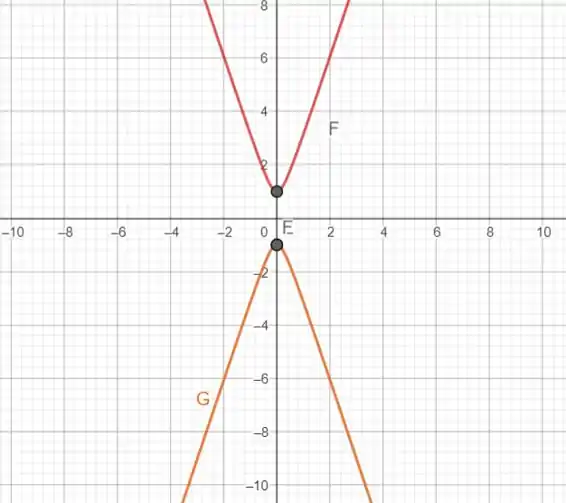
Resposta
Esboço de gráficos.