Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 43c
Para :
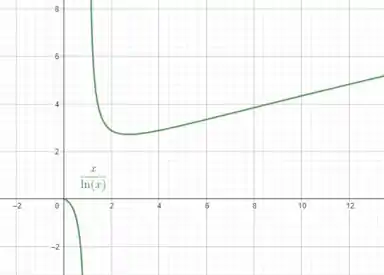
Faça um gráfico de , sabendo:
(i)
(ii)
(iii)
(iv)
Passo 1
Eaee, belezinha?? Bom... O enunciado nos deu a seguinte função:
Queremos esboçar o gráfico de sabendo das seguintes condições:
Vamos verificar o que cada uma dessas condições nos tem a dizer para plotar esse gráfico, certinho??
Ah... é interessante saber que um limite existe em um ponto apenas quando seus limites laterais são iguais nesse ponto 😉
Bora junto aplicar!! 😉
Passo 2
Bom galera, primeiro vamos começar notando que a função não é contínua porque o limite para tendendo a por lados diferentes tem valores diferentes:
Então no ponto a função não é contínua.
Passo 3
Também temos essas condições:
Ou seja, quando se aproxima de zero pela direita, a função tende a zero.
Por outro lado, quando tende ao infinito, a função também tende ao infinito.
Beleza, agora notamos também que ela tem o ponto de início em e o final em .
Agora bora aplicar!! 😉
Passo 4
A gente consegue formar o gráfico:
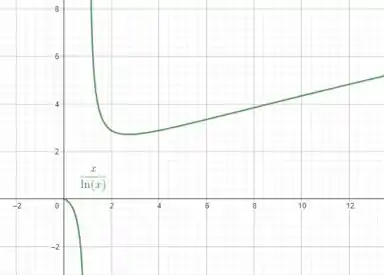
Resposta
