Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 44e
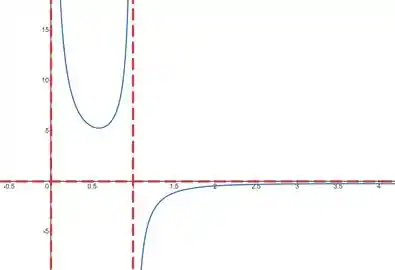
Para , use as informações das partes (a)-(d) para fazer um esboço grosseiro do gráfico de .
(a)
(b)
(c)
(d)
Passo 1
Bom, galera. Essa questãozinha pede pra trabalharmos com essa função aqui:
Basicamente, precisamos fazer um esboço do gráfico dessa função utilizando alguns limites dados. Os limites dados são esses aqui:
(a)
(b)
(c)
(d)
Em primeiro lugar, é importante notar que temos o termo na nossa função e precisamos lembrar que esse termo só está definido para valores positivos de . Ou seja, podemos dizer que o domínio da nossa função é:
Após isso, a grande sacada pra resolvermos essa questão é perceber que os limites dados representam assíntotas. Vamos tentar esboçar essas assíntotas e esboçar o gráfico a partir delas. Vamos lá!
Passo 2
Vamos começar olhando pro primeiro limite dado:
(a)
Temos um limite no infinito () com um resultado finito. Isso tem cara de assíntota horizontal. Ent��o podemos dizer que é uma assíntota hoirizontal!
Vamos começar o nosso esboço traçando essa assíntota:
Legal. Vamos continuar analisando os limites dados.
Passo 3
Vamos checar o próximo limite:
(b)
Agora temos um limite em um número finito () explodindo pro infinito. Agora temos um limite com jeitão de assíntota vertical!
Na verdade, podemos até dizer mais do que isso. Como o nosso limite tende a , sabemos que a nossa curva vai se aproximar dessa assíntota pela parte de cima. Olha só como fica o nosso esboço:
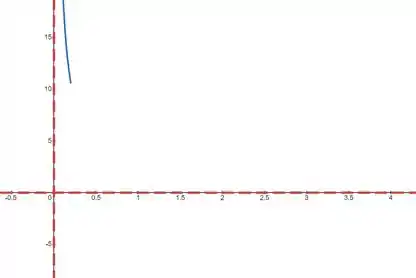
Agora só faltam dois limites!
Passo 4
Vamos ver os dois últimos limites juntos:
(c)
(d)
Essas expressões mostram os limites pela esquerda e pela direita do ponto .
Novamente, temos limites em um ponto finito () explodindo pro infinito, o que sugere que tem uma assíntota vertical aí! Vamos olhar pra cada lado agora.
Do lado esquerdo, de novo temos um limite tendendo a , o que significa que, do lado esquerdo, a nossa curva vai se aproximar da assíntota na parte de cima.
Do lado direito, temos um limite tendendo a . Entção dessa vez, a nossa curva vai se aproximar da assíntota na parte de baixo, pelo lado direito.
Olha só como fica:
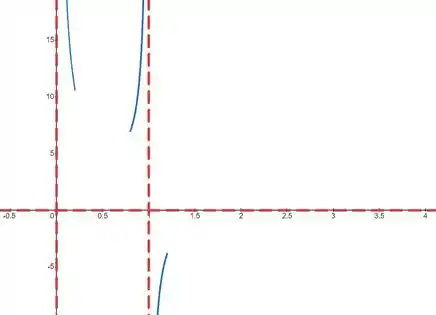
Prontinho! Temos todas as informações que precisamos pra fechar o nosso gráfico!
Passo 5
Lembrando que pra fechar o nosso gráfico, precisamos que a nossa função se aproxime da assíntota horizontal no infinito, temos o seguinte:
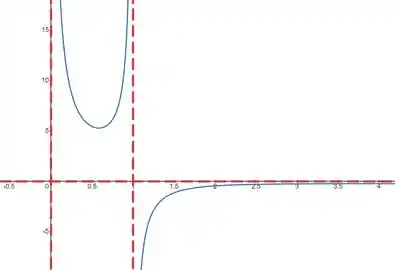
Resposta
