Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.6 - Ex. 16
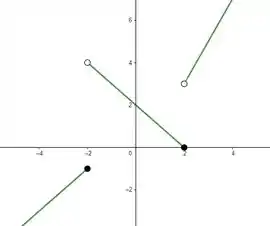
Nos exercícios de a , faça um esboço do gráfico da função; então, observando onde há quebras no gráfico, determine os valores da variável independente nos quais a função é descontínua e mostre por que a Definição não é satisfeita em cada descontinuidade
Passo 1
Tem uma regrinha que dita se uma função é contínua ou não, beleza? A gente faz assim:
E isso vale pra qualquer que a gente escolha. Mas veja bem, como a lei de formação da função só muda em e são exatamente esses pontos que vamos testar, ok? Pro primeiro:
Pro segundo:
Como pros dois casos achamos resultados que não fazem sentido, a função não vai estar definida pra nenhum dos dois valores.
Passo 2
Pra esboçar essa função, note as três leis de formação são retas, mas que não estão definidas nem em nem em . Pra esses pontos temos e . Beleza, então basta desenhar essas retas e tirar os ponto e e adicionar os outros dois:
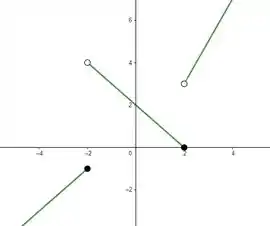
Resposta
Função não é contínua em e em
