Faça o gráfico das três funções , e juntos na mesma tela para e . Para valores maiores de , quais dessas funções possuem os maiores valores e quais possuem os menores valores?

Vamos começar por esboçar os gráficos das funções para . Temos então:

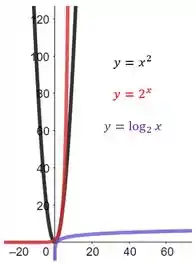
Como pode ser observado, a função é maior para maiores valores de . Já a função é a que possui menores valores.

Vejamos o que acontece agora para o valor de . Temos então:

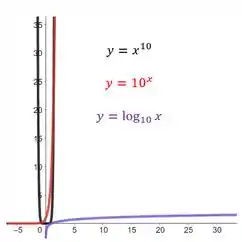
De cara, percebemos que a função é a que possui menores valores à medida que cresce. A grande dúvida é qual possui o maior valor. A partir do gráfico esboçado acima, isto não fica claro. Portanto, precisaremos mudar a escala para melhorar a visualização disto. Vejamos abaixo qual possui o maior valor.

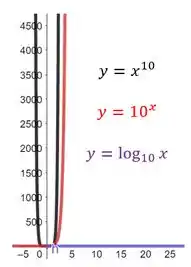
O fato da função estar mais à esquerda do que significa que ela precisa de um menor valor de para atingir o mesmo valor de . Em outras palavras, isto quer dizer que, à medida em que cresce, a função é a que mais cresce!

Para os gráficos das funções quando , acontece o mesmo que quando , isto é, temos que modificar a escala para conseguir visualizar o que a questão nos pede. Vejamos abaixo as curvas com diferentes escalas:

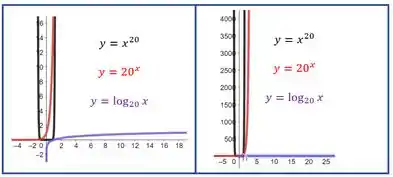
Como pode ser observado, repetiu-se o mesmo fenômeno do passo anterior. A função é a que assume menores valores à medida em que cresce e aquela que assume maiores valores é a função .