Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.6 - Ex. 5

Obtenha gráficos de f que revelem todos os aspectos importantes da curva. Em particular você deve usar os gráficos de f ' e f ' ' para estimar os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão.

f x = x x 3 - x 2 - 4 x + 1

Passo 1

Fala aí! como vai?

Nesse problema foi dada a função

f x = x x 3 - x 2 - 4 x + 1

E nosso objetivo é plotar os gráficos de f ' e f ' ' para estimar os intervalos de inclinação, concavidades, os pontos extremos e os pontos de inflexão...

Parece complicado?

A partir do gráfico de f ' podemos estimar os intervalos de inclinação de f pois essas duas coisas estão diretamente ligadas, ou seja:

  • Quando f ' > 0 a inclinação de f é positiva (crescente) e quando f ' < 0 a inclinação de f é negativa (decrescente).

    • Além disso, a partir de f ' podemos obter os pontos críticos, que são os possíveis valores extremos de f .

    Para obter os pontos críticos, temos que analisar os pontos onde f ' = 0 e para saber se esse ponto é um máximo ou um mínimo, temos que analisar f ' ' .

    Por sua vez, f ' ' está diretamente ligada à concavidade de f , então:

  • Se f ' ' > 0 a função f possui uma concavidade positiva (para cima) e quando f ' ' < 0 a concavidade de f é negativa (para baixo).

    • E por último, vamos analisar os pontos críticos encontrados em f ' = 0 ...

  • Se f ' ' < 0 o ponto é de máximo.
  • Se f ' ' > 0 o ponto é de mínimo.
  • Já os pontos de inflexão acontecem quando f ' ' = 0 .

Show? Bora começar!

Passo 2

Vamos começar calculando a primeira derivada de f ...

f x = x x 3 - x 2 - 4 x + 1

Pela regra do quociente, temos

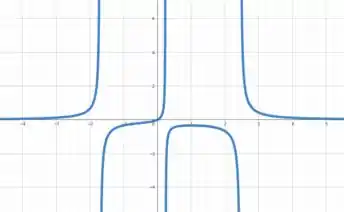
f ' x = d x d x · x 3 - x 2 - 4 x + 1 - x · d x 3 - x 2 - 4 x + 1 d x x 3 - x 2 - 4 x + 1 2

f ' x = - 2 x 3 + x 2 + 1 x 3 - x 2 - 4 x + 1 2

Plotando o gráfico de f ' , temos

Pelo que discutimos no passo 1, podemos estimar que f é crescente em x < 1 pois f ' > 0 e é decrescente em x > 1 pois f ' < 0 .

Além disso, temos apenas um ponto crítico em f , que é justamente em x = 1 pois f ' = 0 nesse ponto.

Show?

Passo 3

Agora vamos repetir o processo para f ' ' ...

Se:

f ' x = - 2 x 3 + x 2 + 1 x 3 - x 2 - 4 x + 1 2

Pela regra do quociente novamente, temos

f ' ' x = d - 2 x 3 + x 2 + 1 d x · x 3 - x 2 - 4 x + 1 2 - - 2 x 3 + x 2 + 1 · d x 3 - x 2 - 4 x + 1 2 d x x 3 - x 2 - 4 x + 1 2 2

Aplicando a regra da cadeia e a regra da potência, chegamos em:

f ' ' x = 2 3 x 5 - 3 x 4 + 5 x 3 - 6 x 2 + 3 x + 4 x 3 - x 2 - 4 x + 1 3

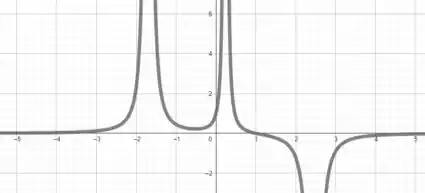
Plotando o gráfico de f ' ' , vamos obter

Perceba que aqui podemos estimar que nos intervalos:

x < - 1,7 - 0,5 < x < 0,2 x > 2,5

A função f possui concavidade voltada para cima pois f ' ' > 0 nesses trechos...

Já nos intervalos:

- 1,7 < x < 0,5   0,2 < x < 2,5

A função f possui concavidade voltada para baixo pois f ' ' < 0 ...

Analisando o ponto crítico que encontramos no passo anterior, temos que em x = 1 , f ' ' < 0 , logo x = 1 é um ponto de máximo em f .

E por último, temos apenas um ponto de inflexão em x = - 0,5 , que é onde f ' ' = 0 .

Tranquilo até aqui?

Passo 4

Para confirmar essas estimativas, vamos plotar o gráfico de f ...

Aqui podemos confirmar os intervalos de inclinação, concavidades, o ponto máximo em x = 1 e o ponto de inflexão que vimos nos passos 2 e 3.

E fim! O que achou? Responde Aí!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,0 ≤ x ≤ 2
A figura mostra os gráficos de f ,f ' ,f ' ' ef ' ' ' . Identifique cada curva e explique suas escolhas.
Use a definição de derivada para encontrar f ' x e f ' ' x . A seguir, trace f ,f 'ef ' ' em uma mesma tela e verifique se suas respostas são razoáveis. f x = 1 / x
A figura mostra o gráfico de três funções. Uma é a função posição de um carro, outra é a velocidade do carro e a outra é sua aceleração. Identifique cada curva e explique suas escolhas.