Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.8 - Ex. 46
Use a definição de derivada para encontrar e . A seguir, trace em uma mesma tela e verifique se suas respostas são razoáveis.
Passo 1
Faaala, gente bonita! Tudo certinho com vocês?
Essa questãozinha pede pra trabalharmos com a definição de derivadas. Então vamos começar relembrando essa expressão:
Iremos utilizar essa relação pra calcular a primeira derivada e a segunda derivada da função .
Mas como fazemos pra achar a segunda derivada com a definição? É só lembrarmos que a segunda derivada é a derivada da própria derivada. Então a definição fica assim:
Após isso, a questão pede pra utilizarmos uma calculadora gráfica para encontrar os gráficos das derivadas e checarmos se são compatíveis com os nossos resultados.
Vamos lá juntos!
Passo 2
Vamos começar calculando a primeira derivada da função usando a definição da derivada:
O termo pode ser escrito da seguinte forma:
Aplicando na definição, temos:
Simplificando a expressão, temos:
Reorganizando a fração:
Legal! Agora podemos aplicar o valor do limite.
Vamos calcular a próxima derivada!
Passo 3
Agora, podemos calcular a segunda derivada!
O termo pode ser escrito assim:
Aplicando na definição, temos:
Simplificando a expressão, temos:
Realizando o produto notável:
Organizando a fração:
Aplicando o limite, temos:
Logo, temos que:
Passo 4
Boa! Conseguimos encontrar os valores da primeira e da segunda derivada da expressão dada:
Agora vamos utilizar uma calculadora gráfica para esboçar os gráficos :
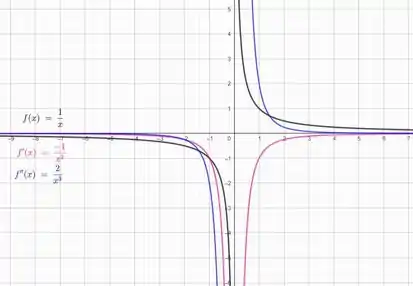
Para avaliarmos se faz sentido com o que encontramos, precisamos lembrar que a derivada de uma função representa a sua taxa de variação. Isso significa que:
Se a função for crescente, sua derivada será positiva.
Se a função for decrescente, sua derivada será negativa.
Percebemos que a função , em preto, tem o seguinte comportamento:
É decrescente pra ;
Não está definida em ;
É decrescente pra .
Isso significa que o gráfico da derivada , em rosa, precisa ter seus sinais da seguinte maneira:
Negativa pra ;
Não estar definida em ;
Negativa pra .
E é exatamente o que encontramos no gráfico. Vamos continuar a nossa análise!
Podemos ver que a derivada tem o seguinte comportamento:
É decrescente pra ;
Não está definida em ;
É decrescente pra .
Isso significa que o gráfico da segunda derivada , em lilás, precisa ter seus sinais da seguinte maneira:
Negativa pra ;
Não estar definida em ;
Positiva pra .
Está batendo com o que encontramos no gráfico! Oba!