Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 51
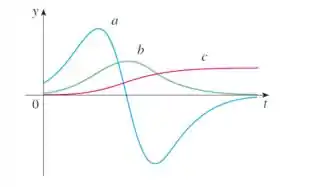
A figura mostra o gráfico de três funções. Uma é a função posição de um carro, outra é a velocidade do carro e a outra é sua aceleração. Identifique cada curva e explique suas escolhas.
Passo 1
E aí, pessoal! Nesse problema temos o gráfico:
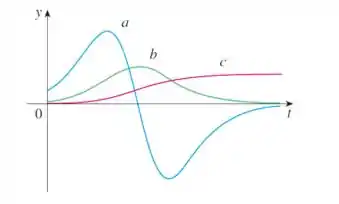
Uma curva é a posição de um carro ao longo do tempo, a outra é a sua velocidade e outra a aceleração. Nosso desafio aqui é descobrir quem é quem!
Para resolver esse problema temos que lembrar de uma propriedade muito importante...Qual a relação entre a função posição e a função velocidade?
A função velocidade é a derivada da função posição e a função aceleração é a derivada da função velocidade! Ou seja:
Show, mas e aí, como que a gente faz?
Temos que lembrar que, quando uma função esta crescendo a sua derivada é positiva, quando ela ta decrescendo a derivada é negativa!
Passo 2
Vamos trazer o gráfico pra pertinho:
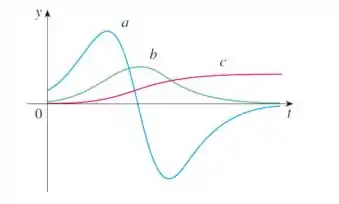
Como um chute inicial podemos imaginar que o carro ta sempre andando pra frente. Vamos sair desse palpite e ir vendo se conseguimos construir uma coerência!
Se o carro ta sempre indo pra frente então faz sentido a curva ser a posição.
Beleza, sua inclinação é sempre positiva. No início a inclinação é maior, depois começa a diminuir e mais pro final ela parece ficar constante, inicando que o carro parou.
Então a sua derivada deve ser sempre positiva, no início ela vai ser maior e depois vai diminuir e vai se aproximar de . A curva que bate com essa descrição é a , portanto:
Sobrou a aceleração, que é a derivada da velocidade. Vamos ver se a curva é coerente!
A curva tem a parte incial com inclinação positiva e a outra parte com a inclinação negativa, então a sua derivada deve ter a primeira parte positiva e a segunda negativa! Bate certinho, temos:
Resumondo temos:
E aí! o que achou? Responde Aí!