Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.1 - Ex. 20
Esboce o gráfico de à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de .
Passo 1
Oieeee, bora resolver mais uma comigo
Vamos esboçar o gráfico da função no intervalo e determinar os valores máximos e mínimos locais e absolutos.
Vamos analisar a Função
A função é uma parábola que abre para cima com vértice na origem No intervalo estamos interessados na parte da parábola entre e .
Os pontos críticos dentro do intervalo são as extremidades do intervalo.
Para :
Para próximo de
Passo 2
Para esboçar o gráfico de no intervalo
1. Plote o ponto e
2. Desenhe a parábola que passa por esses pontos, sendo côncava para cima.
- Máximo absoluto: O valor máximo absoluto ocorre em ;
- Mínimo absoluto: O valor mínimo absoluto ocorre em
Passo 3
Para desenhar o gráfico à mão:
1. Plote o ponto e
2. Desenhe a parábola que passa por esses pontos.
Gráfico:
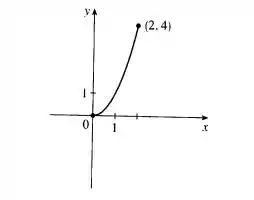
Passo 4
- Máximo absoluto: em
- Mínimo absoluto: em
Dentro do intervalo , a função tem um valor mínimo absoluto de em e um valor máximo absoluto de em . Não há outros máximos ou mínimos locais dentro desse intervalo, pois a função é monotonamente crescente no intervalo que nos foi fornecido.
Resposta
Vide o passo a passo.