Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.1 - Ex. 18
Faça uma tabela de valores para a função nos pontos , , , , e .
- Determine a taxa média de variação de nos intervalos para cada em sua tabela.
- Qual é a taxa média de crescimento dos lucros entre 2002 e 2004?
- Utilize o gráfico para estimar a taxa em que os lucros variaram em 2002.
Passo 1
A primeira coisa que vamos fazer é uma tabela de valors para .
Lembrando que o coeficiente angular é calculado por:
Assim,
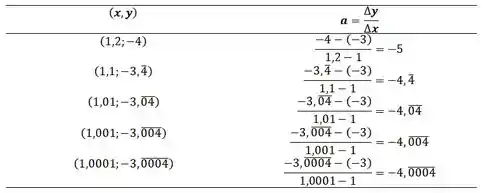
Passo 2
Como podemos ver pela letra a.), o coeficiente angular tende a quando vamos diminuindo o valor de para valores próximos a , portanto
Resposta
Exercícios de Livros Relacionados
Seja Determine lim x → 0 + f ( x ) Em caso afirmativo, qual é? Em caso negativo por que não?Determine lim x → 0 - f ( x ) Em caso afirmativo, qual é? Em caso negativo por que não?Determine lim x →
Seja f x = { 3 - x ,x2 x 2 + 1 , x2 Determine lim x → 2 + f ( x ) e lim x → 2 - f ( x ) .Existe lim x → 2 f ( x ) ? Em caso afirmativo, qual é? Em caso negativo por que não?Determine lim x → 4 -
9- Faça os gráficos das funções nos Exercícios 9 e 10. Em seguida, responda às questões.Qual é o domínio e a imagem de f ?Em que pontos c , se houver, lim x → c f ( x ) existe?Em que pontos existe o
51- Defina o que significa dizer lim x → 0 g x = k .
73. Seja g ( θ ) = ( sen θ ) / θ .a. Faça uma tabela dos valores de g em valores de θ que se aproximam de θ 0 = 0 por cima e por baixo. Em seguida, estime lim θ → 0 g ( θ )