Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.4 - Ex. 9
9-
Faça os gráficos das funções nos Exercícios 9 e 10. Em seguida, responda às questões.
- Qual é o domínio e a imagem de ?
- Em que pontos , se houver, existe?
- Em que pontos existe o limite a esquerda?
- Em que pontos existe o limite a direita?
Passo 1
O gráfico da primeira linha pode ser encontrado da seguinte forma:
O que nos dá a equação característica de uma circunferência de raio 1. Só que como ele originalmente ele nos forneceu a raiz positiva de y então temos a semicircunferência positiva só que limitada de 0 a 1, onde incluo o zero e excluo o 1, da seguinte forma em roxo no gráfico abaixo.
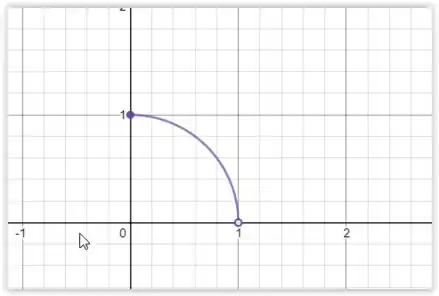
A segunda nos diz que temos o valor 1 indo de x de 1 a 2, onde incluo 1 e não incluo 2 como está em vermelho.
Agora a terceira só inclui o ponto como está em laranja.
Passo 2
Letra a)
O domínio é tudo aquilo que é representável no eixo e por mais que tenhamos alguns pontos abertos em alguns pontos temos também pontos fechados nesses mesmos pontos, logo nosso domínio é:
Não se esquecendo de incluir esses pontos, já que temos bolinha fechada neles. Só não incluir caso fosse até infinito.
Já a imagem é tudo aquilo que se encontra no eixo e a mesma tem um alcance limitado de 0 a 1 e depois ele pula para 2:
e
Onde temos bolinha aberta em .
Passo 3
Letras b)
A função possui dois intervalos bem definidos pela quebra de continuidade que são:
Então temos que analisar os limites nos pontos em
Em :
Pela esquerda temos a semicircunferência que tende a dar 0.
E pela direita a reta , que nos fornece o valor igual a 1.
Como os limites são diferentes então não temos a bilateralidade
Como a letra b quer saber os valores de nas quais eu possuo a bilateralidade, então tenho que descartar , assim como o ponto não possui limite a esquerda e o ponto não possui limite pela direita:
Passo 4
Letra c)
Como pede-se quais pontos tem o limite a esquerda, logo podemos ver que somente não o possui pois não existe gráfico a esquerda desse ponto, logo nosso domínio fica:
Letra d)
Como agora pede-se quais que tem limite a direita, fica-se evidente que em não temos gráfico para poder dizer o seu limite a direita nos dando o seguinte domínio:
Resposta
- Domínio: , Imagem: e