Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 54

A face de um dique adjacente à água está inclinada 45 ° em relação à vertical. A face é um retângulo com 80   m de largura e 40   m do lado inclinado. Se o dique estiver cheio de água, ache a força total na face devido à pressão de água.

Passo 1

Um esquema da placa inclinada é mostrado na figura:

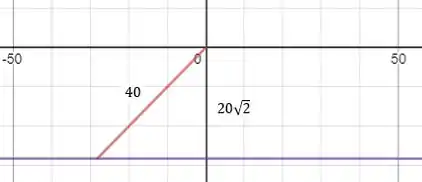
Usamos para modelar a placa a reta y = x com x ≤ 0 . Como o comprimento da placa é 40   m , temos que - 20 2 ≤ x ≤ 0 e - 20 2 ≤ y ≤ 0 . A largura de 80   m está no plano perpendicular ao desenho (“para dentro”).

Consideremos uma faixa fina na superfície da placa com área:

Δ A = 80 ⋅ 2   Δ y

O fator 2 vem da projeção do eixo y sobre a placa inclinada. A força que age sobre essa faixa é

p y i = ρ g 0 - y i = - ρ g y i

Assim, a força sobre essa faixa será

Δ F i = - ρ g y i   Δ A = - 80 2 ρ g   y i   Δ y

Somando a força em cada faixa e fazendo Δ y → 0 , obtemos a seguinte integral para a força:

F = - 80 2 ρ g   ∫ - 20 2 0 y   d y

Passo 2

Fazendo a integração:

F = - 80 2   ρ g   y 2 2 - 20 2 0

Assim,

F = - 80 2   ρ g ⋅ - 400 ⋅ 2 2

Portanto,

F = 32000 2 ρ g

Passo 3

Usando ρ = 100 0   k g / m 3 e g = 9,8   m / s 2 , temos que

F ≈ 4,43 ⋅ 10 8   N

Resposta

4,43 ⋅ 10 8   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Ent
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Ent
Um tanque tem 8 metros de comprimento, 4 de largura e 2 de altura e contém querosene com densidade de 820k g / m 3 até uma profundidade de 1,5 metros. Descubra (a) a pressão hidrostática no fundo do t
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Ent
Um cubo com lados de 20c m de comprimento está no fundo de um aquário no qual a água atinge 1 m de profundidade. Calcule a força hidrostática (a) no topo do cubo e (b) em um dos lados do cubo.