Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 31
Fazer um esboço do gráfico de , determinando:
. Os extremos relativos de ;
. Os pontos de inflexão do gráfico de ;
. Os intervalos onde é crescente e aqueles nos quais é decrescente;
. Onde o gráfico é côncavo para cima e onde é côncavo para baixo;
Da função dentro do intervalo de
Passo 1
Legal gente, sem pânico! Temos milhões de coisas pra calcularmos, então vamos ser organizados e dividir tudo em pequenos passos de cada vez. A primeira coisa que a questão nos pede, é que determinemos os extremos relativos de f. Para isso, temos que:
- Fazer a primeira derivada e igualar a 0 para achar um c
- Fazer a segunda derivada e realizar um teste para determinamos se é um extremo ou mínimo relativo.
Então, nossa função é dada por:
Derivando e igualando a 0, temos que:
Resolvendo essa equação, observamos que as raízes são para todo x (considerando “n” um número inteiro qualquer):
Passo 2
Ufa, primeira parte já foi! Para a segunda parte, precisamos definir o nosso ponto de inflexão. Resumindo, vamos derivar 3 vezes e achar esses pontos? PREPARADOS? SIMBORA!
Neste ponto, igualamos a 0 e temos nossos primeiros candidatos a pontos de inflexão.
Agora derivamos mais uma vez, e verificamos que se o nosso x for diferente de 0, os nossos pontos achados acima são pontos de inflexão.
Percebemos então que os nossos pontos de:
São pontos de inflexão. Isso é normal gente, existem n pontos de inflexão porque a nossa função é uma senóide. Então toda vez que ela toca o 0, ela muda de concavidade, logo tem “n” pontos de inflexão.
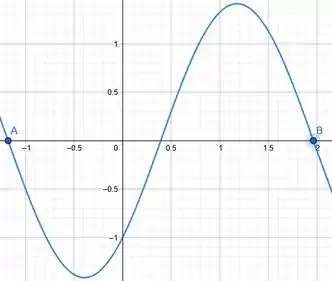
Passo 3
Observamos pelo gráfico acima, que ela decresce de e a partir dai sobe até . Sendo assim as nossas concavidades.
Resposta
Extremos relativos:
Pontos de inflexão: