Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.7 - Ex. 54
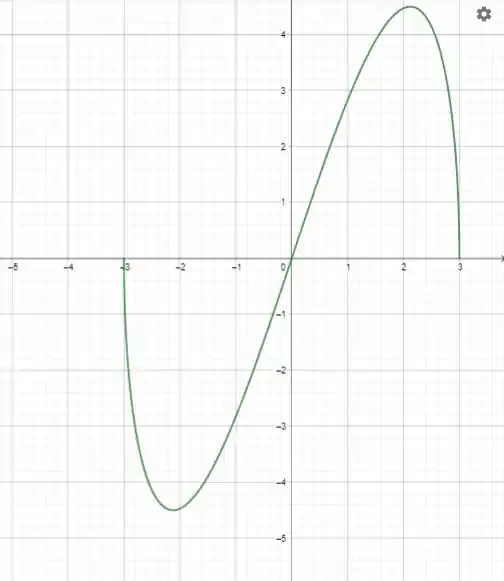
Ache as assíntotas horizontal e vertical do gráfico de , determinando o seguinte:
Os extremos relativos de ;
Os pontos de inflexão do gráfico de ;
Os intervalos em que é crescente
Os intervalos em que é decrescente;
Onde o gráfico é côncavo para cima;
Onde o gráfico é côncavo para baixo;
A inclinação de qualquer tangente de inflexão;
As assíntotas horizontal, vertical e oblíqua, se existirem
Passo 1
Essa função tem domínio sendo:
Vamos para as assíntotas:
Vamos começar pela assíntota horizontal.
Assíntota horizontal: fazer o limite no infinito. Ou seja,
Como esta entra e , não teremos assíntota com nem
Tanto na horizontal quanto na oblíqua
Passo 2
Vamos para as verticais. Para isso, temos que procurar algum valor de que faça o limite ir para . Normalmente procuramos quando o denominador da fração for . Aqui, temos uma potencia racional, que é uma fração na potência. Nesses casos não teremos assíntotas verticais.
Passo 3
Vamos aos extremos e os intervalos de crescimento e decrescimento. Para isso temos que analisar o sinal de .
Derivando usando a regra do produto, vamos ter:
Como é sempre positivo, vamos ter:
A raiz do denominador é sempre positiva, então o sinal depende só de . Vamos olahr seu gráfico:
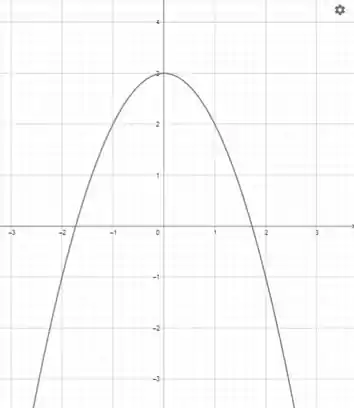
Entre as raízes vai ser positivo, e fora vai ser negativo. Mas o nosso
Lembrando que a função vai só de até , então o intervalo fica:
Lembrando que o domínio limita a função em
A função é crescente se e decrescente se , então:
Passo 4
Agora vamos ver os extremos. Pelo teste da primeira derivada, teremos máximo quando a função vai de crescente para decrescente, e mínimo quando a função for de decrescente para crescente.
Passo 5
Vamos agora para a concavidade e os pontos de inflexão. A função é côncava para cima se e côncava para baixo se .
O ponto vai ser de inflexão quando muda a concavidade.
Vamos pegar
Usando a regra do quociente:
Podemos não colocar o módulo ali no denominador, porque o domínio dizque é positivo
Colocando em evidência:
Como está entre e , e , vamos ter que é sempre negativo.
O nosso denominador vai ser sempre positivo.
O sinal da segunda derivada vai depender só de:
Então:
Esse ssinais vão trocar ao olhar a derivada, porque o é negativo:
LEbrmando que o nosso domínio para em
Então:
Assim, é ponto de inflexão:
Passo 6
Para terminar vamos ao esboço. Para isso, precisamos juntar todas as informações.
Não possui assíntota
ponto de inflexão
O gráfico vai ficar:
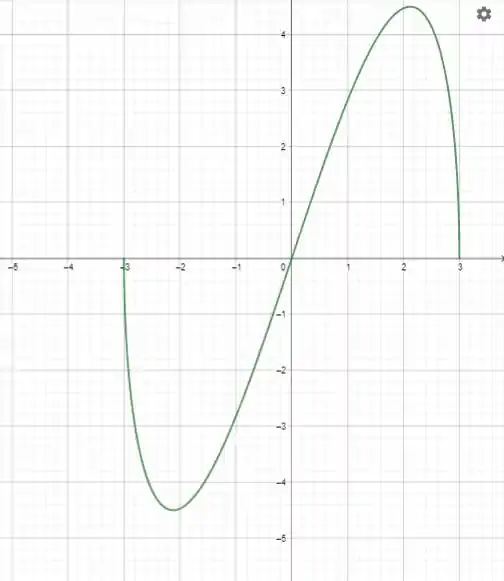
Resposta
Não possui assíntota
ponto de inflexão
O gráfico vai ficar:
