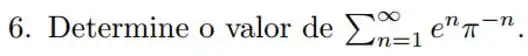Exercícios de Série geométrica - Lista de Exercícios Resolvida

A série

é convergente? Caso positivo, calcule a sua soma (o limite das somas parciais).

Calcule a soma da série:

Classifique as afirmações abaixo em verdadeiras ou falsas, justificando suas respostas:

Diga se a série abaixo converge ou diverge. No caso da série convergir, calcular o valor da soma.

A série é convergente ou divergente?

Mostre que

Dada a série

É correto afirmar que:

1. É uma série geométrica
3. A série converge a
4. A série converge a
6. A série diverge

2) Quais das séries convergem e quais divergem? Se uma série convergir, calcule a sua soma.

c)

2) Quais das séries convergem e quais divergem? Se uma série convergir, calcule a sua soma.

a)

2) Quais das séries convergem e quais divergem? Se uma série convergir, calcule a sua soma.

d)

2) Quais das séries convergem e quais divergem? Se uma série convergir, calcule a sua soma.

f)

2) Quais das séries convergem e quais divergem? Se uma série convergir, calcule a sua soma.

i)

2) Quais das séries convergem e quais divergem? Se uma série convergir, calcule a sua soma.

g)

2) Quais das séries convergem e quais divergem? Se uma série convergir, calcule a sua soma.

h)

3) Ache os valores de para os quais a série geométrica dada converge. Encontre também a soma das séries (como uma função de ) para esses valores de .

a)

3) Ache os valores de para os quais a série geométrica dada converge. Encontre também a soma das séries (como uma função de ) para esses valores de .

b)

3) Ache os valores de para os quais a série geométrica dada converge. Encontre também a soma das séries (como uma função de ) para esses valores de .

c)

4) Usando série geométrica, expresse as dízimas periódicas abaixo como o quociente entre dois inteiros

a)

4) Usando série geométrica, expresse as dízimas periódicas abaixo como o quociente entre dois inteiros

b)

Calcule a soma da série

Calcule a soma de

Determine a soma da série geométrica

Determine a soma da série geométrica

2) Quais das séries convergem e quais divergem? Se uma série convergir, calcule a sua soma.

e)

Calcule a soma da série

Calcule a soma da série:

Classifique as afirmações abaixo em verdadeiras ou falsas, justificando suas respostas:

Calcule a soma de

Considere a série

em que , e são números reais fixados (constantes).

A série é geométrica? Justifique sua resposta.

Se a série for geométrica, encontre condições sobre , e para que a série seja convergente.

a) Determine se a série converge e se convergir calcule a sua soma:

Calcule a soma de

Dizer se a série converge ou diverge. No caso da série convergir, calcular o valor de sua soma.

Questão 3 (Justifique todas as suas respostas):

1. Considere a série

Em que , e são constantes.

Determine se esta é uma série geométrica; determine uma relação entre e para que a série seja convergente.

2) Quais das séries convergem e quais divergem? Se uma série convergir, calcule a sua soma.

b)

Seja a sequência numérica definida por e . Considere as seguintes afirmações:

(I) é sequência monótona crescente.

(II) é limitada superiormente por .

(III) .

Podemos afirmar que:

a) Apenas as afirmações (I) e (II) são verdadeiras.

b) Apenas a afirmação (II) é verdadeira.

c) Todas as afirmações são verdadeiras.

d) Apenas a afirmação (III) é verdadeira.

e) Apenas a afirmação (I) é verdadeira.

Seja . Qual é o limite ?

Escolha uma opção:

Determine o valor de para que

Calcule a soma da série:

Encontre a soma da série