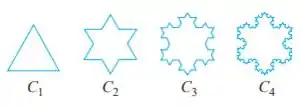
Curva do floco de neve de Helga von Koch. A curva do floco de neve de Helga von Koch é uma curva de comprimento infinito que engloba uma região de área finita. Para entender a razão disso, imagine que a curva é gerada a partir de um triângulo equilátero cujos lados têm comprimento igual a .

1. Encontre a área da região circundada por e mostre que .

Oi galera, vem comigo no passo a passo deste exercício!

Neste exercício queremos encontrar o a área . Sabemos que a área de um triângulo equilátero de lado é dado por:

E a área da curva é a soma das áreas geradas pelos novos triângulos que surgem a cada passo. Assim, podemos escrever que:

em que cada é a área dos novos triângulos.

Então vamos lá! Na primeira curva () temos:

Já na segunda curva (), são acrescentados 3 novos triângulos cada um com a seguinte área:

E na curva () são adicionados quatro novos triângulos, de aresta , para cada aresta do triângulo original, sendo assim:

Equivalentemente temos:

E consequentemente, percebemos que: