Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 70
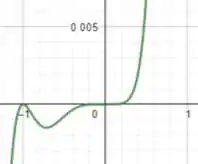
A figura Ex-70 mostra o gráfico do polinômio gerado em um computador usando uma janela de . Mostre que a escolha da janela vertical faz com que o computador perca aspectos importantes do gráfico. Encontre os aspectos omitidos e faça seu próprio esboço mostrando-os.
Passo 1
Então pessoal, a princípio não sabemos quais são esses aspectos importantes que são omitidos no gráfico, então a fim de determinarmos isso vamos ver se a função apresenta pontos de máximos e/ou mínimos, pois essas são as únicas possibilidades de resposta! Nossa função é:
Derivando para encontrarmos os pontos críticos:
Igualando a derivada a zero, teremos:
Para isso dar zero:
Da primeira tiramos que , da segunda tiramos que e da terceira tiramos que .
Passo 2
Ok, determinamos pontos críticos e isso é importante para nossa resposta! Agora precisamos determinar se são pontos de máximos ou mínimos, ok? Para temos:
Como a derivada passa de crescente para decrescente, isso implica que é um ponto de máximo. Para temos:
Como a derivada passa de decrescente para crescente, isso implica que é um ponto de mínimo. Por fim, para não conseguimos afirmar nada sobre a derivada, pois a mesma não muda de sinal. Olha que loucuraaaaa! Encontramos pontos de máximo e mínimo e isso não aparece no gráfico! Sendo assim, para esse comportamento aparecer devemos dar um zoom, ficando com o gráfico assim:
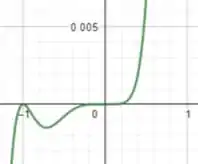
E aí estão as informações omitidas no gráfico do enunciado!
Resposta
