Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.1 - Ex. 32
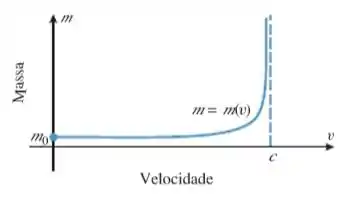
Na Teoria Especial de Relatividade, a massa de um objeto em movimento é uma função da velocidade do objeto. A Figura Ex-32, em que denota a velocidade da luz, exibe algumas das características qualitativas dessa função.
(a) Qual a interpretação física de ?
(b) Qual é o ? Qual é o significado físico desse limite?
Passo 1
Não é nosso objetivo aqui adentrar no assunto da Teoria da Relatividade, mas, vejamos uma coisa interessante: a teoria prevê que, em velocidades suficientemente altas, próximas à da luz, um objeto vai ter sua massa aumentada com o aumento dessa velocidade!
Resposta
(a)Fica fácil entender que nada mais é que a massa original do objeto, em repouso!
(b)O significado é a aproximação da velocidade do objeto à velocidade da luz, que, de modo geral, não é atingível pra objetos macroscópicos. Porém, se fosse, o objeto estaria cada vez mais ganhando massa, oferecendo resistência ao aumento da velocidade, cada vez mais.