Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.8 - Ex. 4

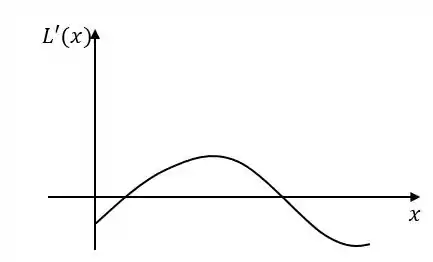
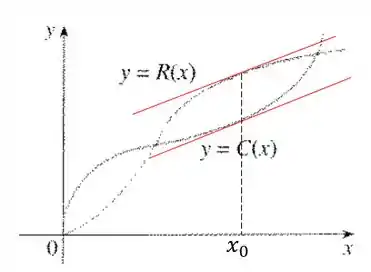
A figura mostra os gráficos das funções custo e rendimento registrados por um fabricante.

  1. Identifique sobre o gráfico o valor de x para o qual o lucro é maximizado.
  2. Esboce o gráfico da função lucro.
  3. Esboce o gráfico da função lucro marginal.

Passo 1

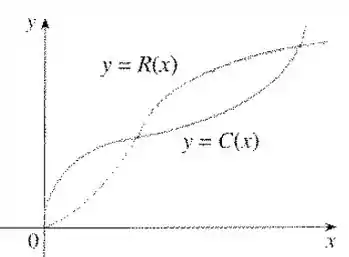
(a) Para que o lucro seja maximizado, o custo marginal deve ser igual ao rendimento marginal, ou seja:

C ' x = R ' ( x )

Isso significa que as retas tangentes à curva de R e de C devem ter a mesma inclinação, ou seja, ser paralelas. Procurando então no gráfico encontramos o ponto:

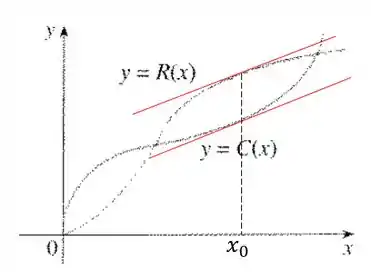
Podemos confirmar que esse é um ponto de máximo pois se deslocarmos para a direita ou para a esquerda teremos uma diminuição da distância entre R ( x ) e C ( x ) . Essa distância representa o lucro.

Passo 2

(b) A função lucro é dada pelo rendimento menos o custo total:

L x = R x - C ( x )

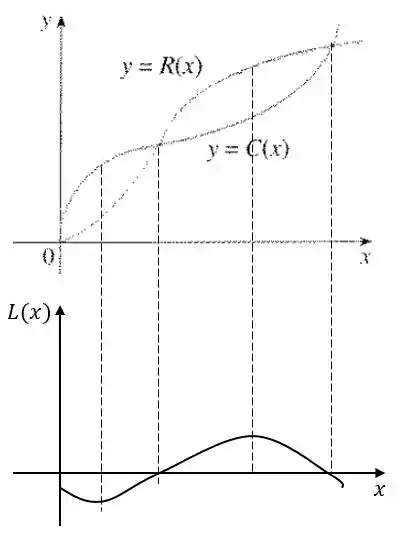
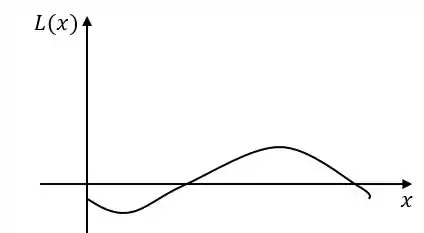
Primeiro R ( x ) é zero e C ( x ) positivo: temos um lucro negativo (prejuízo). A distância entre as curvas fica maior (prejuízo aumenta) até um máximo, e depois começa a diminuir. Em um ponto R x = C ( x ) e o lucro é zero. Após isso a distância entre as curvas aumenta até o lucro máximo e depois diminui para zero novamente. Nosso gráfico então fica assim:

Passo 3

(c) Para esboçar o gráfico do lucro marginal L ' ( x ) usamos o gráfico esboçado de L ( x ) . Ele começa negativo, vai a zero no ponto de prejuízo máximo, depois aumenta e começa a diminuir novamente, passando pelo zero no lucro máximo.

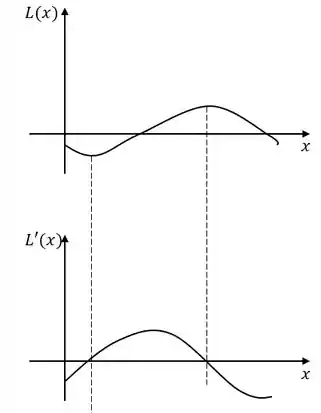
Resposta

(a)

(b)

(c)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

10 O movimento de uma partícula é ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância da partícula a partir de um pontoO , em t s. A direção positiva é à direita. De
12 O movimento de uma partícula é ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância da partícula a partir de um pontoO , em t s. A direção positiva é à direita. De
13. O movimento de uma partícula é ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância da partícula a partir de um pontoO , em t s. A direção positiva é à direita. D
11. O movimento de uma partícula é ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância da partícula a partir de um pontoO , em t s. A direção positiva é à direita. D
14 O movimento de uma partícula é ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância da partícula a partir de um pontoO , em t s. A direção positiva é à direita. De