Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 59
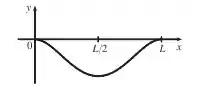
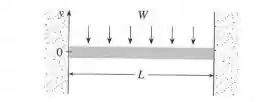
A figura mostra uma viga de comprimento embutida entre paredes de concreto. Se uma carga constante for distribuída uniformemente ao longo de seu comprimento, a viga assumirá a forma da curva de deflexão
em que e são constantes positivas. ( é o módulo de elasticidade de Young, e é o momento de inércia da secção transversal da viga.) Esboce o gráfico da curva de deflexão.
Passo 1
Bom galera, nessa questão queremos esboçar o gráfico da curva de deflexão.
A curva de deflexão é dada por:
Para isso, utilizaremos os conceitos desse capítulo para auxiliar a esboçar o gráfico.
Vamos procurar pela derivada dessa função e assim verificar onde ela cresce e decresce, pois ela é crescente se
E decrescente se
Vamos procurar por pontos onde que esses podem ser pontos de máximo ou mínimo locais.
Por fim, vamos encontrar a segunda derivada para verificar a concavidade da função. Ela será côncava para cima se
E ela será côncava para baixo se
Com isso, já conseguimos esboçar a nossa função.
Ah, também é bom a gente reparar que essa função é definida num domínio que vai de até . Ou seja, não precisamos olhar para assíntotas horizontais, afinal a função não tende a nenhum infinito.
Passo 2
Podemos simplificar a função da seguinte maneira
Colocando o em evidência, temos:
Podemos aqui perceber que ali temos um produto notável do tipo:
Sendo que no nosso caso temos:
Aplicando a nossa função, temos:
E para ficar mais enxuto ainda, fazemos:
Talvez antes de começarmos, vale a pena verificarmos o valor dessa função nos seus extremos, isso é, quando e quando .
Beleza, vemos portanto que nos extremos a função vale .
Passo 3
Vamos derivar a nossa função.
Temos que
Derivando temos uma regra do produto:
Vamos colocar o em evidência:
Avaliando o sinal dessa derivada , lembrando que varia de até apenas:
�� um fator que sempre é negativo.
é sempre positivo.
é sempre negativo.
Para o fator , temos:
Portanto, quando o fator é positivo, multiplicado por um fator negativo, um positivo e um negativo, temos uma derivada que é positiva e a função cresce.
E, quando , o fator é negativo, multiplicado por um fator negativo, um positivo e um negativo, temos uma derivada que é negativa e a função decresce.
é portanto um ponto crítico. Como a função decrescia e depois passa a crescer esse é um ponto de mínimo local.
Passo 4
A primeira derivada é:
Vamos ajeitar antes de derivar de novo:
Tomando a segunda derivada temos:
Organizando:
Para verificar o sinal da segunda derivada, precisamos verificar o sinal da função de segundo grau. Encontrando suas raízes temos:
Como essa função de segundo grau possui , ela é côncava para cima, portanto ela é positiva quando e e ela é negativa quando .
Como a constante que multiplica a função de segundo grau é uma constante negativa, temos que a será negativa quando e . E que ela será positiva quando .
Os pontos de inflexão são e .
Dessa forma, já conseguimos traçar a nossa curva .
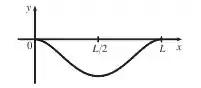
Percebe que de até temos concavidade para baixo.
De até temos concavidade para cima.
Depois de até temos concavidade para baixo novamente.
A função decresce de até quando chega em seu mínimo e depois cresce de até .
Resposta
