- Escreva uma equação que defina a função exponencial com base
- Qual é o domínio dessa função?
- Se , qual a imagem dessa função?
- Esboce a forma geral do gráfico da função exponencial nos seguintes casos.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente (a) escrever uma equação que defina uma função exponencial com base posita, , (b) determinar o domínio dessa função, (c) determinar a sua imagem considerando e (d) esboçar a forma geral do gráfico da função exponencial para os casos:
Então, vamos lembrar da definição de função exponencial, que tem sempre uma base positiva e uma variável no expoente. Determinar seu domínio, considerando todos os valores que pode assumir na função e determinar sua imagem, considerando todos os valores que irá assumir na função.
E por fim, vamos esboçar o gráfico da função exponencial nos intervalos onde a base é positiva, onde ela é igual a e quando ela está entre e .
Vamos lá!
Passo 2
(a) O que nós precisamos lembrar é que a função exponencial, em geral, tem a forma:
onde é uma constante positiva () e o seu expoente é a sua variável, por definição.
É importante a gente perceber também que o exercício define que a base deve ser positiva porque, quando é uma fração, teremos uma raiz. E quando o denominador dessa fração for par, teremos uma raiz de índice par (como a raiz quadrada), que não aceita números negativos no radicando. Então, para garantir que não vamos ter problema com isso, a base tem que ser positiva, beleza?
Passo 3
Agora, para a letra (b) queremos o domínio da função .
Nesse caso, a variável pode assumir qualquer valor entre os números reais.
Se for uma fração, vai ser uma raiz. Exemplo:
Se for negativo, vamos ter uma inversão:
Se for não depende do valor de :
Então, o domínio é o conjunto dos reais mesmo.
Passo 4
Na letra (c) queremos definir a imagem de , considerando .
Para isso, lembra que a base é positiva? Então, não vai poder assumir valores negativos, porque uma potência (ou raiz, se o expoente for uma fração) de um número positivo será sempre outro número positivo.
Como não existe número que elevado a outro que dê zero, o também não pertence à imagem da . E imagem é, então definida no intervalo aberto:
Passo 5
Por último, na letra (d), queremos a forma geral do gráfico. Isso quer dizer que vamos ter que esboçar, indicar apenas a forma, nada exato.
Para (i) , a função vai crescer muito rápido conforme vai aumentando.
Quando , a função é
,
porque qualquer número elevado a zero é um. Ou seja, independentemente do valor de , a função vai valer em . Isso quer dizer que a curva da exponencial vai cortar o eixo no ponto e gráfico, então, fica assim:
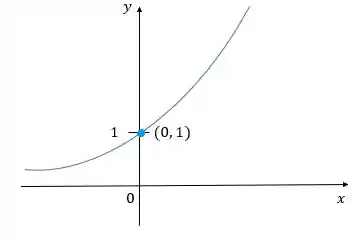
Passo 6
Para (ii) , a função vai ser constante, porque nossa função será:
,
Já que elevado a qualquer número é .
Dessa forma, o gráfico de é uma reta horizontal em :
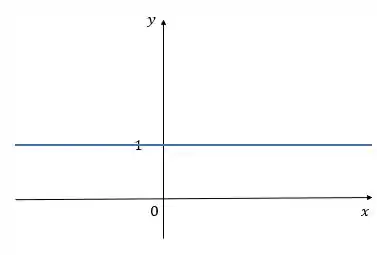
Passo 7
Para (iii) , teremos como um número decimal, certo?
Então quanto mais aumentamos o valor de , menor fica. Exemplo:
Então, a função será descrescente, e tocará o eixo no ponto , como vimos no primeiro caso.
Sendo assim, nosso gráfico tem a forma:
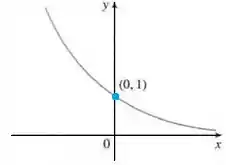
Valeu, galera! Até a próxima! 😉
Resposta
(a)
(b) Domínio:
(c) Imagem:
(d) (i) (ii) (iii)