Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.3 - Ex. 57
Um navio se move a uma velocidade de paralelo a uma costa retilínea. O navio está a da costa e passa por um farol ao meio-dia.
- Expresse a distância entre o farol e o navio como uma função de , a distância que o navio percorreu desde o meio-dia; ou seja, encontre tal que
- Expresse como uma função de , o tempo decorrido desde o meio-dia; ou seja, encontre tal que .
- Encontre O que esta função representa?
Passo 1
Eaee, belezinha?? Bom... a questão nos diz que um navio se move a uma velocidade de paralelo a uma costa retilínea. O navio está a da costa e passa por um farol ao meio-dia.
Queremos montar uma função que expresse a distância entre o farol e o navio como uma função de , a distância que o navio percorreu desde o meio-dia.
Depois queremos expressar como uma função de , o tempo decorrido desde o meio-dia.
Por fim, queremos encontrar a função composta e dizer o que ela representa.
Mas antes, vamos olhar na figura para entender melhor a questão:
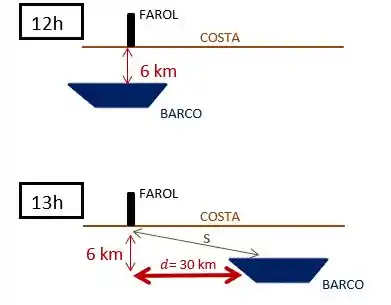
Agora vamos lá!! 😉
Passo 2
A gente pode ver que se forma um triângulo retângulo na figura:
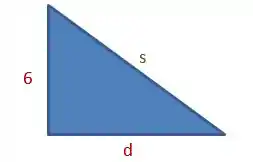
Assim, a distância entre o navio e o farol é, pelo teorema de Pitágoras:
Assim, a função que queremos em (a) é
Passo 3
Agora, para a letra (b), queremos uma função que expresse a distância que o navio percorreu desde o meio-dia, de acordo com o tempo que se passou desde esse horário.
Como foi dito que ele percorre em uma hora, basta pegar o tempo (em horas) que se passou desde o meio dia e multiplicar pela quantidade que ele percorre em uma hora (
Essa vai ser a função , que descreve a distância
Passo 4
Por último, em (c), queremos a função composta . Basta substituir toda variável da função de pela função inteira de
Okay, beleza, mas o que isso representa?
A função é uma forma de descobrir a distância entre o navio e o farol somente através do tempo decorrido desde o meio-dia, sem precisar calcular a distância que o navio já percorreu!!
Fazemos isso porque sabemos que a distância que o navio percorreu segue a regra de uma função, então não precisamos passar por esse passo toda vez que quisermos descobrir a distância entre o navio e o farol.
É um jeito de deixar o cálculo mais direto e rápido!
Entendeu direitinho?? Responde aee 😉
Resposta
- , que é a distânciaentre o navio e o farol de acordo com o tempo decorrido desde as 12h.