Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.1 - Ex. 48
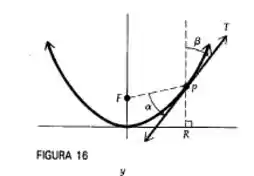
48. Na Figura 16, prove que . (Sugestão: escolha os eixos coordenados de tal forma que a parábola tenha seu vértice na origem e seu eixo ao longo do eixo y e que se abra para cima. Seja Q a intersecção da reta tangente PT com eixo y. Prove que , mostrando que é isósceles.)
Passo 1
O enunciado nos sugere uma forma de provar a igualdade, mas não necessariamente temos que seguir essa sugestão. Vamos usar um triangulo isósceles também para provar a igualdade, mas não é o mesmo do enunciado.
A imagem a seguir representa a situação que o enunciado nos fornece.
Passo 2
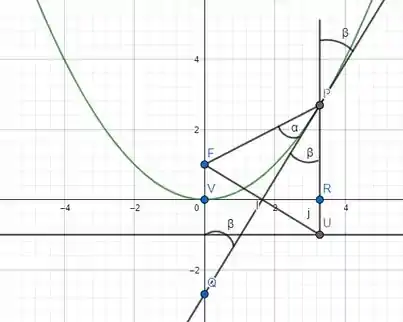
Vamos usar o , já que através das propriedades da parábola podemos saber que dois lados desse triangulo são iguais.
A definição de parábola diz que a distância entre um ponto qualquer da parábola e o foco é igual a distância desse mesmo ponto a reta diretriz. Assim, observando a figura vemos que PU é igual a PF, assim confirmamos que é isósceles.
Passo 3
Podemos ver que a reta tangente é a bissetriz do , e pela propriedade dos triângulos isósceles, que diz que a bissetriz do ângulo entre os lados iguais do triangulo isósceles divide esse ângulo em duas partes iguais.
Uma dessas partes é o ângulo e o outro é o ângulo , podemos saber isso graças a seguinte relação:
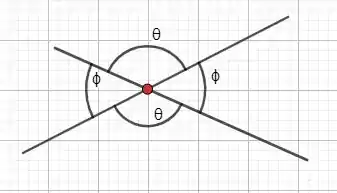
As duas partes que a reta bissetriz divide o ângulo são iguais, logo .
Resposta
Ei, a resposta está no passo a passo :)