Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 76
Prove que o ponto médio de todas as cordas pararelas a uma corda fixa estão sobre uma reta pararela ao eixo da parábola.
Passo 1
Vamos primeiro desenhar nossa parábola, para então termos o que trabalhar em cima!
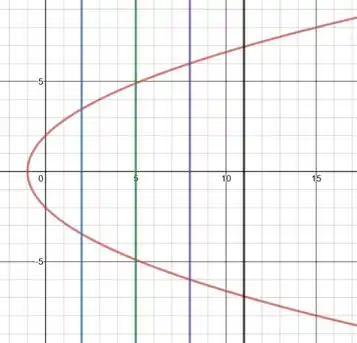
A gente observa que toda corda é pararela a nossa primeira corda azul, porque:
Como a nossa parábola é simétrica em x, então:
Em que d representa a distancia do ponto médio até a cônica.
Passo 2
Podemos observar a mesma coisa com essa imagem.
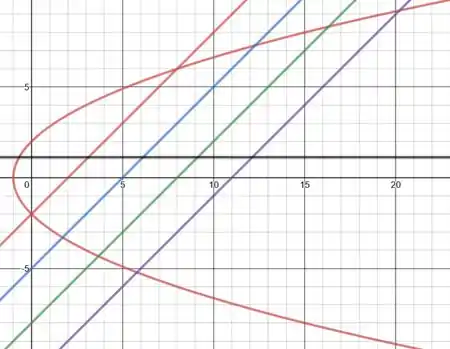
Em que todas as cordas estão com um ângulo, mas o ponto médio continua pararelo ao eixo da parábola, pois segue a mesma regra:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos Exercícios 13 a 20, o gráfico da equação dada é uma elipse ou uma hipérbole. Ache o centro, vértices e focos da cônica. Se o gráfico for uma elipse, ache também as extremidades do eixo menor. Se o
Nos Exercícios 13 a 20, o gráfico da equação dada é uma elipse ou uma hipérbole. Ache o centro, vértices e focos da cônica. Se o gráfico for uma elipse, ache também as extremidades do eixo menor. Se o
A região “triangular” no primeiro quadrante delimitado pelo eixo x, a reta x = 4 e a hipérbole 9x2 - 4y2 = 36 é girada em torno do eixo x para gerar um sólido. Encontre o volume do sólido.
Encontre o centroide da região que é delimitado abaixo pelo eixo x e acima pela elipse (x2/9) + (y2/16) = 1.
Encontre as dimensões do retângulo de maior área que podem ser inscritos na elipse x2 + 4y2 = 4 com seus lados paralelos aos eixos coordenados. Qual é a área do retângulo?