Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.3 - Ex. 14
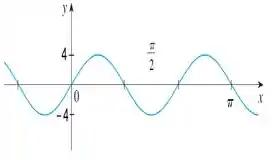
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção e então aplicando as transformações apropriadas.
Passo 1
Hello hello hello!
Bom, nós temos um gráfico pra traçar, mas precisamos usar as funções de referência do livro, então vamos começar relembrando dessas funções.
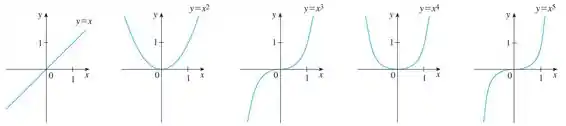
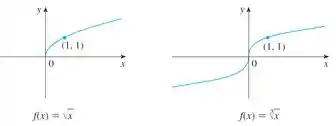
Calma, não precisa surtar com esse monte de gráfico! O negócio aqui é tentar identificar qual delas é mais parecida, o que elas tem em comum e o que tem, de diferente!
Qual você acha mais parecida com a nossa ?
Bom, essa é uma função seno ne, então não é muito difícil perceber que a melhor escolha é a função
Agora vamos pro passo 2 falar das transformações.
Passo 2
Bom, pra nós temos:
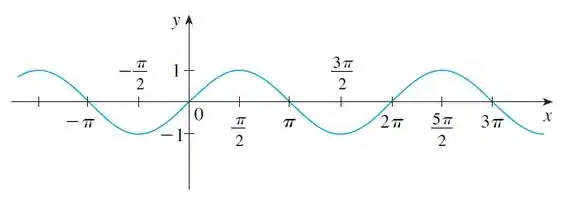
E queremos o gráfico de
Parece bem difícil né? Más não! Olha só, bebê...
Tem muitas formas de transformar funções e a multiplicação por constantes costuma gerar algum tipo de contração no gráfico ou faz ele ficar esticado em alguma direção.
Quando multiplicamos por 3, o que estamos dizendo é que precisamos de um valor 3 vezes menor pra obter o mesmo resultado, então é como se a gente contraísse a função horizontalmente.
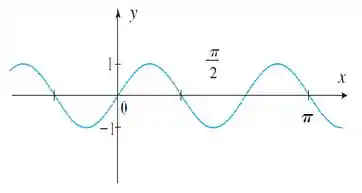
Parece igualzinho, mas repara nos valores do eixo
Passo 3
Agora vamos partir do gráfico de , pra achar:
Quando a gente multiplica o por 4, a gente tá quadruplicando o valor do seno, é como expandir a função em 4 verticalmente.
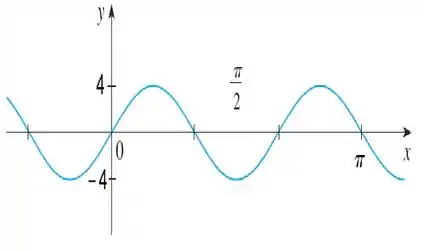
UFA! Achamos!
Resposta
