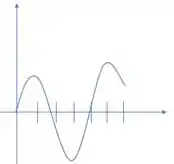
A figura a seguir mostra o gráfico velocidade versus tempo, para uma partícula movendo-se ao longo de um eixo coordenado. Faça um esboço dos gráficos velocidade escalar versus tempo e aceleração versus tempo.
Passo 1
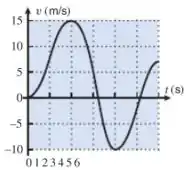
Então pessoal, o enunciado nos cede um gráfico de velocidade versus tempo e nos pede o esboço do gráfico de velocidade escalar versus tempo? Como assim? Pois bem galera, quando falamos de velocidade escalar, estamos falando do módulo da velocidade, ou seja, uma curva de velocidade escalar versus tempo não admite velocidades negativas. Tendo isso em vista, basta espelharmos a parte negativa do gráfico em torno do eixo e pronto, se liguem:
Passo 2
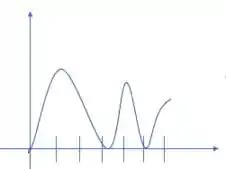
Tudo bem, a primeira parte foi feita! Sabemos que a aceleração é a derivada da velocidade em função do tempo, não é mesmo? Então o que devemos fazer é analisar a derivada da função que nos foi dada através do gráfico. Temos os seguintes intervalos:
a derivada é positiva;
a derivada começa a decrescer;
ponto de máximo;
a derivada é decrescente;
a velocidade é nula;
a derivada é crescente novamente;
a velocidade é nula.
Tendo em vista esses dados, temos que um esboço seria:
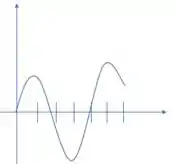
E está aí nossa resolução, galera!
Resposta
Velocidade escalar versus tempo:
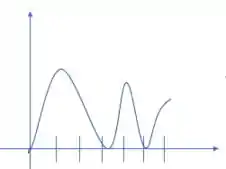
Aceleração versus tempo: