Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.5 - Ex. 16

Esboce o gráfico.

y = sqrt(x^2 + 2 x + 5)

Passo 1

Note que o domínio dessa função é toda a reta real, pois:

x^2 + 2 x + 5 > 0 AA x

Vamos derivar para achar os intervalos de crescimento e decrescimento:

y^' = (2 x + 2)/(2 sqrt(x^2 + 2 x + 5)) = (x + 1)/(sqrt(x^2 + 2 x + 5))

Como a raiz quadrada é sempre positiva, teremos crescimento quando:

x + 1 > 0 => x > - 1

E decrescimento quando:

x + 1 < 0 => x < - 1

Assim, x = 1 corresponderá a um ponto de mínimo local.

Passo 2

Para estudar a concavidade, vamos derivar novamente:

y^(' ') = (sqrt(x^2 + 2 x + 5) - (x + 1) ((x + 1)/(sqrt(x^2 + 2 x + 5))))/(x^2 + 2 x + 5) = (x^2 + 2 x + 5 - (x + 1)^2)/((x^2 + 2 x + 5) sqrt(x^2 + 2 x + 5)) = (4)/((x^2 + 2 x + 5)^((3)/(2)))

Logo,

y^(' ') > 0 AA x

Ou seja, a concavidade do gráfico é sempre para cima.

Passo 3

Repare que quando x -> +- oo , temos y -> + oo . Então, aparentemente, não há assíntotas. Porém, veja que:

underset(x -> +- oo)(lim) (y)/(x) = underset(x -> +- oo)(lim) (sqrt(x^2 + 2 x + 5))/(x) = underset(x -> +- oo)(lim) +- sqrt(1 + (2)/(x) + (5)/(x^2)) = +- 1

Ou seja, teremos as seguintes retas assíntotas oblíquas:

(y)/(x) = +- 1

Passo 4

Agora já temos um bocado de informação sobre o gráfico da função. Bora fazer o esboço?

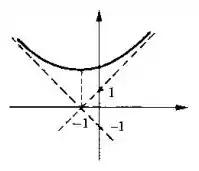
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o gráfico das funções racionais nos Exercícios 85-102.92- y = x 2 - 4 x 2 - 2
Identifique os pontos de inflexão e os máximos e mínimos locais da função representada graficamente. Identifique os intervalos em que a função é côncava para cima e aqueles em que ela é côncava para b
Identifique os pontos de inflexão e os máximos e mínimos locais da função representada graficamente. Identifique os intervalos em que a função é côncava para cima e aqueles em que ela é côncava para b
Represente graficamente a equação seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflex
Represente graficamente a equação seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflex