Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.10 - Ex. 12

Um fluido escoa em movimento uniforme no domínio D = { x , y 0 ≤ y ≤ 8 } . Se a velocidade em cada ponto é dado por v → = y + 1 i → , verificar que todas as partículas se deslocam em linha reta e que v → representa um possível fluido incompressível.

Passo 1

Queremos identificar se o fluido é incompressível, ou compressível, para isso precisamos calcular div ⁡ v → . Isso é porque, pela equação da continuidade

div ⁡ u → + ∂ ρ ∂ t = 0

∂ ρ ∂ t = - div ⁡ u →

o fluido será incompressível se div ⁡ u → = 0 .

Passo 2

Queremos encontrar div ⁡ v → , então basta fazermos o seguinte:

div ⁡ v → = ∂ v 1 ∂ x + ∂ v 2 ∂ y + ∂ v 3 ∂ z

Aplicando a formula cima em v → temos:

div ⁡ v → = ∂ ∂ x y + 1 + ∂ ∂ y 0 + ∂ ∂ z 0

div ⁡ v → = 0 - 0 + 0

div ⁡ v → = 0

Temos então que o fluido é incompressível.

Passo 3

Para verificar que todas as partículas se deslocam em linha reta, podemos analisar a representação gráfica do campo vetorial v → na figura abaixo.

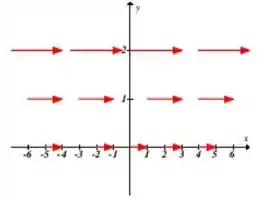
Podemos aqui concluir, que todas as partículas se deslocam em linha reta.

Resposta

Fluido incompressível.

div ⁡ v → = 0

Todas as partículas se deslocam em linha reta.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fluido escoa em movimento uniforme com velocidade v → dada. Verificar se v → representa um possível fluxo incompressível. v → = 2i → + xj → -k →
Dado o campo vetorial f → , calcular d i vf → . f → x ,y ,z = ln ⁡ x yi → + xj → + zk →
Um fluido escoa em movimento uniforme com velocidade v → dada. Verificar se v → representa um possível fluxo incompressível. v → = 2 x yi → + xj →
Supondo que v → representa a velocidade de um fluido em movimento, verificar se v → representa um possível fluido incompressível.d) v → x , y = - y , x
Seja u → = x 2 - y 2 ⋅ ∇ f . Calcular div ⁡ u → no ponto P ( 1 , 2,3 ) sendo:b) f = x y z + 2 x y