Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 16
Uma folha de papelão mede . Dois quadrados iguais são recortados dos vértices de um lado com , como mostra a figura. Dois retângulos iguais são recortados dos outros vértices, de modo que as abas possam ser dobradas para formar uma caixa retangular com tampa.
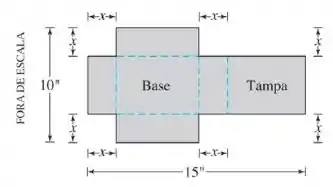
Escreva uma fórmula para o volume da caixa.
Determine o domínio de para esse problema e esboce o gráfico de nesse domínio.
Use um método gráfico para determinar o volume máximo e o valor respectivo de que o fornece.
Confirme o resultado que você obteve no ítem analiticamente.
Passo 1
Letra
Vamos primeiro entender como é a situação. Ele pegou uma folha e cortou quadrados nas pontas.
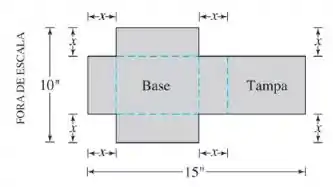
Pela figura podemos, quando dobrarmos a caixa vamos ter:
Fazemso aquela divisão por porque temos o comprimento da base e da tampa, junto com dando os , então como queremos um so temos que dividir a diferença por
E seu volume vai ser o produto dessas medidas.
Passo 2
Vamos ter que a fórmula do volume vai ser
Abrindo essa conta, vamos ter:
Passo 3
Letra
Só um pequeno detalhe, aquele tem um intervalo que ele vale. Isso porque ele é uma medida, então precisa ser positiva.
Além disso, os dois lados da caixa precisam ser positivos, fazendo com que:
E
Assim, vamos ter
Assim, devemos ter:
Esse é o domínio.
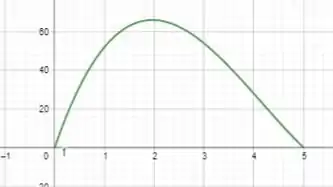
Usando o geogebra para fazer o gráfico de , vamos ter:
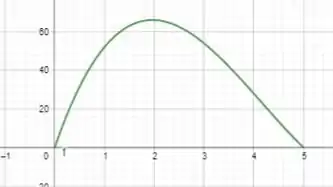
Passo 4
Letra
Ainda a partir do uso do geogebra, vamos ter:
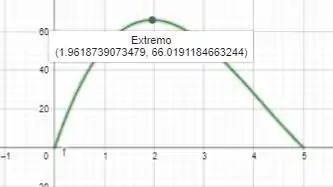
Então o volume máximo é quando
Passo 5
Letra
Para achar o maior possível, temos que achar o ponto de máximo de .
Para isso, temos que ver se existe algum ponto de máximo ou mínimo no intervalo de e comparar com os valores extremos do intervalo de
Vamos começar achando a derivada:
Ela vai ser em:
Aplicando Bhaskaras:
Teremos:
Ou
Apenas o segundo valor está no intervalo de que queremos, para isso vamos jogar isso na calculadora tá? Rs
Aproveitar que ele pedu varias contas com método gráfico.
então vamos focar só nele como ponto crítico.
Passo 6
Achamos o nosso ponto crítico. Vamos usar o teste da segunda derivada para conferir se ele é máximo ou mínimo ou nada rs
Vamos ver o valor da segunda derivada em .
Como a derivada deu negativa, pelo teste da segunda derivada, é valor de máximo local.
Passo 7
Vamos comparar agora os valores de em , que são os extremos do intervalo e o máximo local. Vamos usar a fórmula antes de fazer a distribuitiva porque é mais fácil de fazer conta:
Vamos usar uma calculadora aqui porque tem uma raiz ali no meio e ele só quer comparar mesmo os valores.
Então vamos ter que a área máxima é .
Resposta
Letra
Letra
Letra
o volume máximo é quando