Um cone circular reto deve ser inscrito em uma esfera com um dado raio. Ache a razão entre a altura e o raio da base do cone de maior volume possível.
Passo 1
Visualizar o problema
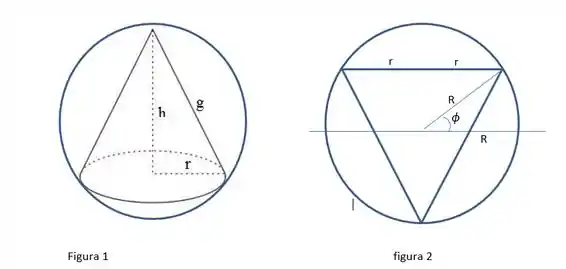
Passo 2
Visualizamdo a figura 2, um corte Transversal. Podemos observar que o raio do cone (rc) é limitado pelo raio da esfera (Re), assim como também h é limitado pelo raio da esfera. Logo podemos fazer r e h como função da esfera.
r varia em relação ao ângulo , logo podemos escrever r = Rcos , visto que r é a projeção horizontal de R, se olharmos para o circulo ( figura 2 )
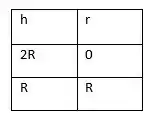
Para acharmos h podemos montar uma tabelinha, e ver como ele varia com r
Logo podemos escrever h como R + Rsen, logo h = R ( 1 + sen, com .
(Em teoria poderia ser entre , contudo como queremos o maior volume possível
Não nos interessa o intervalo já que nessa parte r seria menor que R. Visto que
Sendo o Volume Cone = 1/3 h . Area da Base =
V =
V=
Passo 3
Otimizando nosso problema .
Logo
O que nos leva a :
Visto que são constantes
Passo 4
Uma solução então é
Continuando a solução
Visto que cos²x + sen²x = 1
Fazendo u = , temos :
Então temos que cos
O que nos leva a
Tanto 90° quanto 270°, são valores que não nos interresam pois fornecem volume do cone = 0
(r = Rcos )
Entao o ângulo procurado é 19,5°.
Passo 5
Queremos h/r
Sendo h = R ( 1 + sen,
r = Rcos
logo
h/r = =
Plotando nosso
h/r = =
Resposta
h/r =